El volumen es una medida que calcula el espacio que ocupa un cuerpo geométrico (de tres dimensiones). También se puede entender como el espacio comprendido dentro del área de un cuerpo geométrico. La capacidad es un concepto equivalente al volumen, pero se refiere al volumen que puede contener un recipiente o cuerpo vacío.
Las medidas del volumen son unidades de distancia al cubo (ej: cm3, m3,…).
¿Cómo se calcula el volumen?
El volumen, generalmente, se calcula a partir de las tres magnitudes de un cuerpo de tres dimensiones: altura, ancho y largo. Pero dependiendo de la figura que estemos estudiando, se calculará a partir de diferentes fórmulas, como veremos a continuación.
Volumen del prisma
El volumen de un prisma es el producto del área de la base (Ab) por la altura del prisma (h). En un prisma recto la altura coincide con una altura lateral, mientras que en un prisma oblicuo no.


Prisma triangular regular

El volumen de un prisma triangular es el producto del área del triángulo equilátero de una de sus bases por la altura (h).
El prisma triangular regular es un prisma recto que tiene como bases dos triángulos equiláteros.

Prisma cuadrangular regular

El prisma cuadrangular regular es un prisma recto que tiene como bases dos cuadrados.
El volumen de un prisma cuadrangular es el producto del área del cuadrado de una de sus bases por la altura (h).

Prisma pentagonal regular

El volumen de un prisma pentagonal es el producto del área del pentágono regular de una de sus bases por la altura (h).
El prisma pentagonal regular es un prisma recto que tiene como bases dos pentágonos regulares.

Prisma hexagonal regular

El volumen de un prisma hexagonal es el producto del área del hexágono regular de una de sus bases por la altura (h).
El prisma hexagonal regular es un prisma recto que tiene como bases dos hexágonos regulares.

Volumen de la pirámide
El volumen de una pirámide es un tercio del área de la base de la pirámide (Ab) y su altura (h).


Pirámide regular

La pirámide regular tiene como base un polígono regular y es recta. Sea una pirámide regular con la base de N aristas.
La fórmula del volumen de la pirámide regular es:

Pirámide triangular
Pirámide triangular regular


Pirámide triangular irregular


Pirámide cuadrangular
Pirámide cuadrangular regular
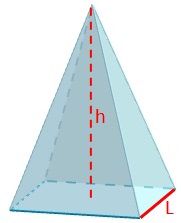

Pirámide cuadrangular irregular


Pirámide pentagonal
Pirámide pentagonal regular


Pirámide pentagonal irregular


Pirámide hexagonal
Pirámide hexagonal regular


Pirámide hexagonal irregular


Principio de Cavalieri
Si sólidos iguales en altura, al ser cortados por cualquier plano paralelo a sus bases se producen en ellos secciones de igual área, entonces esos sólidos tendrán el mismo volumen.

El principio (o teorema) de Cavalieri declara la igualdad de los volúmenes de cuerpos de formas diferentes, siempre que cumplan sus dos exigencias: igual altura e igual área en secciones producidas mediante un plano cualquiera paralelo a la base.
Volumen de un poliedro regular
Tetraedro

El volumen de un tetraedro se calcula a partir de una de sus aristas (a):

Cubo (hexaedro regular)

El volumen de un cubo (o hexaedro regular) es igual a la longitud de sus aristas al cubo:

Octaedro

El volumen de un octaedro (u octoedro) se calcula mediante la fórmula siguiente:

Dodecaedro

El volumen de un dodecaedro se calcula sabiendo la longitud de la arista, mediante la fórmula siguiente:

Icosaedro

El volumen de un icosaedro se puede calcular a partir de una de sus aristas, mediante la fórmula siguiente:

Esfera

El volumen de una esfera se calcula en función de su radio (r). Su fórmula es:

Cilindro

El volumen de un cilindro se calcula mediante la fórmula:

Cono

La fórmula general del volumen de un cono es:

Que es la misma fórmula que la del volumen de la pirámide.
En el caso del cono de base circular, tanto recto como oblicuo, su volumen será:

Tronco del cono

El volumen de un tronco de cono se calcula con la fórmula:

Toro
El volumen del toro se calcula mediante la fórmula:


Donde R es el radio de la circunferencia directriz y r el del círculo generatriz.
Esta fórmula es una aplicación del segundo teorema de Pappus-Guldin, donde el centroide de su sección círculo es su centro.

es de gran utilidad
thanks
Me gusta mucho la información útil pero tengo una pequeña queja y es que no está el volumen del rombo
El rombo es un polígono, una figura plana sin volumen.
Pero y el prisma del rombo?
Consulta la página Prisma cuadrangular en UNIVERSO FÓRMULAS.
El prisma cuyas bases son rombos está en el apartado Prisma cuadrangular irregular
es una buena informacion
estuvo muy chido, la informacion me ayudo bastante
me facilito hacer la tarea porque con el profesor no le entendi yo que de haci¿¿??
perfect
Están todos menos el octágono
me ayudo bastante amigos gracias por todo me saque 05 en el examen mentira era una broma mañana daré examen
SERA UN RESULTADO MUY BIEN
esta muy bien esta informacion muy completa
esta muy buena su pagina gracias por la informavion
me encanto esto ya que me ayudo a hacer mi tarea y me saco de un apuro aunque deberían aumentarle mas cuerpos geométricos por crear esta pagina web
gracias