
El cubo (o hexaedro regular) es un poliedro regular compuesto por seis cuadrados iguales.
Es uno de los cinco sólidos platónicos.
Según el Teorema de Euler para poliedros, el hexaedro regular tiene seis caras, doce aristas y ocho vértices.
A cada vértice del cubo concurren tres caras
Un cubo tiene cuatro diagonales.
En este cuadro se reflejan estos elementos, del hexaedro y del resto de poliedros:

Siendo:
- C, el número de caras del poliedro.
- V, el número de sus vértices.
- A, las aristas.
- D, las diagonales.
Área del cubo (o hexaedro regular)

El cálculo del área del cubo es muy sencillo a partir de una arista:

¿Cómo se obtiene la fórmula?
En efecto, como cada una de las seis caras son cuadrados, vemos en área del cuadrado que su área es:
Como el cubo tiene seis cuadrados por caras:
Hallar el área de un cubo conociendo la diagonal

Si el dato que se conoce es la diagonal del cubo.
Mediante la fórmula de la diagonal del cubo se puede despejar el valor de la arista a y aplicar la fórmula conocida del área del cubo:

Hallar el área de un cubo conociendo su volumen

Si el dato que se conoce es el volumen del cubo:
Empleando la fórmula del volumen del cubo se puede despejar igualmente el valor de la arista a y aplicar la fórmula conocida del área del cubo:

Volumen del cubo (o hexaedro regular)

El volumen del cubo es igual a la longitud de sus aristas al cubo:

¿Cómo se obtiene la fórmula?
Como el cubo es también un prisma recto cuadrangular, si vemos el volumen del prisma es:
El área de la base Ab se halla por la fórmula del área del cuadrado y es: Ab = a2.
Por tanto, el volumen del cubo, con la fórmula del prisma será:
Diagonal del cubo
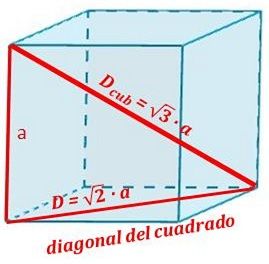
Las diagonales de un cubo son rectas que unen vértices que pertenecen a caras diferentes. En particular el cubo tiene cuatro diagonales.
Para saber la longitud de estas diagonales, aplicaremos al triángulo rectángulo de la figura, el teorema de Pitágoras. Un cateto es una arista, el otro cateto es la diagonal de una cara (Diagonales del cuadrado).
La hipotenusa será la diagonal del cubo buscada y la fórmula para calcularla es:

La fórmula para hallar el número de diagonales de un poliedro regular es:

Siendo C es el número de caras del poliedro, V, el número de sus vértices, A, las aristas y D, las diagonales.
No se tienen en cuenta las diagonales de los polígonos de las caras DCT que tienen L lados. Estas diagonales de los polígonos se obtiene con la fórmula:

Una sección del cubo
Si cortamos un cubo con un plano perpendicular a una diagonal del mismo en su punto medio, este plano cortará seis aristas del cubo también en su centro. La sección será un hexágono cuyo lado será igual a la mitad de la diagonal de una cara del cubo

¿Sabias qué los poliedros regulares se conocen también como sólidos perfectos o sólidos platónicos? Se conocen desde la antigüedad clásica. Aunque le atribuyen a Pitágoras (569 a.C. – 475 a.C). el descubrimiento de los cuatro primeros y su escuela el restante, fué Platón (427 a.C – 347 a.C.) quien los cita en sus Diálogos. Les da un carácter místico, asociándolos a los elementos de la filosofía clásica: al tetraedro, el fuego, al cubo, la tierra, al octaedro, el aire, al dodecaedro, los límites del universo y al icosaedro, el agua.

pues me sirvio por que me dejaron una tarea de investigar su clasificaciones y pues me sirvio de mucho, muchas gracias
Esto me ayudo demasiado sobre mi tarea ya que en una clase falte y fue justo cuando explicaron esto muchísimas gracias muy excelente información gracias.
Esta pagina me ayudo a hacer mi tarea
Muy buena información gracias
chevere
tengo una tarea de volumen y esto me ayudo un poco mas informacion no estaria mal.
no tienen elementos
Yo tengo 12 años y tengo que a ser un álbum de los poliedros regulares le recomendaria que colocaran los cincos poliedros me ayudo esta pagina pero un poquito más de información seria mejor
muy buenas teorias
excelente universo de formulas
tienes razon keyla tine buenas dimensiones