Las funciones trigonometricas son aquellas que están asociadas a una razón trigonométrica.

Las razones trigonométricas de un ángulo α son las obtenidas entre los tres lados de un triángulo rectángulo. Es decir, las comparaciones por su cociente de sus tres lados a, b y c.
Existen seis funciones trigonométricas:
Seno

El seno de un ángulo α se define como la razón entre el cateto opuesto (a) y la hipotenusa (c).

Su abreviatura son sen o sin (del latín sinus).
La gráfica de la función seno es:
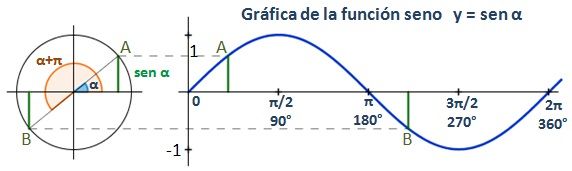
La función del seno es periódica de período 360º (2π radianes), por lo que esta sección de la gráfica se repetirá en los diferentes períodos.
- Dominio:

- Codominio:

- Derivada de la función seno:

- Integral de la función seno:

Coseno

El coseno de un ángulo α se define como la razón entre el cateto contiguo o cateto adyacente (b) y la hipotenusa (c).

Su abreviatura es cos (del latín cosinus).
La gráfica de la función coseno es:

La función del coseno es periódica de período 360º (2π radianes).
- Dominio:

- Codominio:

- Derivada de la función coseno:

- Integral de la función coseno:

Tangente

La tangente de un ángulo α es la razón entre el cateto opuesto (a) y el cateto contiguo o cateto adyacente (b).

Su abreviatura son tan o tg.
La gráfica de la función tangente es:

La función de la tangente es periódica de período 180º (π radianes).
- Dominio:
 (excepto π/2 + a · π), siendo a un número entero. O, con esta casuística: x ≠ ±π/2; ±3π/2; ±5π/2;…
(excepto π/2 + a · π), siendo a un número entero. O, con esta casuística: x ≠ ±π/2; ±3π/2; ±5π/2;… - Codominio:

- Derivada de la función tangente:

- Integral de la función tangente:

Cosecante

La cosecante es la razón trigonométrica recíproca del seno, es decir csc α · sen α=1.
La cosecante del ángulo α de un triángulo rectángulo se define como la razón entre la hipotenusa (c) y el cateto opuesto (a).

Su abreviatura es csc o cosec.
La gráfica de la función cosecante es:

La función de la cosecante es periódica de período 360º (2π radianes).
- Dominio:
 (excepto a · π), siendo a un número entero.
(excepto a · π), siendo a un número entero. - Codominio:

- Derivada de la función cosecante:

- Integral de la función cosecante:

Secante

La secante es la razón trigonométrica recíproca del coseno, es decir sec α · cos α=1.
La secante de un ángulo α de un triángulo rectángulo se define como la razón entre la hipotenusa (c) y el cateto contiguo o cateto adyacente (b).

Su abreviatura es sec.
La gráfica de la función secante es:

La función de la secante es periódica de período 360º (2π radianes).
- Dominio:
 (excepto π/2 + a · π), siendo a un número entero. O, con esta casuística: x ≠ ±π/2; ±3π/2; ±5π/2;…
(excepto π/2 + a · π), siendo a un número entero. O, con esta casuística: x ≠ ±π/2; ±3π/2; ±5π/2;… - Codominio:

- Derivada de la función secante:

- Integral de la función secante:

Cotangente

La cotangente es la razón trigonométrica recíproca de la tangente, por lo tanto tan α · cot α=1.
La cotangente de un ángulo α de un triángulo rectángulo se define como la razón entre el cateto contiguo o cateto adyacente (b) y el cateto opuesto (a).

Su abreviatura es cot, cotg o cotan.
La gráfica de la función cotangente es:

La función de la cotangente es periódica de período 180º (π radianes).
- Dominio:
 (excepto a · π), siendo a un número entero.
(excepto a · π), siendo a un número entero. - Codominio:

- Derivada de la función cotangente:

- Integral de la función cotangente:


Excelente pagina, fue de gran ayuda.
También tiene información completa, espero encontrarme más paginas como esta.
Excelente trabajo 👍
Ejemplos muy claros, muchas gracias.
no me gusta estudiar deta
por favor ponle autor y fechaaa, gracias por la información.
Excelente página, me has ayudado mucho, te agradezco. Saludos.
Muchas gracias fue de gran ayuda para mi .
Excelente
Qué relación hay entre una función trigonometríca y los logaritmos?
nolose pro deberias a ponerte a leer
los logaritmos son los valores determinados de las funciones trigonometricas
No, Anael, no es así.
Otra cosa es resolver funciones trigonométricas exponenciales por logaritmos, pero estamos en otro tema.
Normalmente tomo varias páginas para mis investigaciones, y hacer una buena y completa. ¡Me gustaría encontrarme con más páginas y con explicaciones así! Gracias, es de gran utilidad.
Impresionante, gracias 😀
que bueno xddd
oye tonto es xdxd
muchisimas gracias me ayudo en mi tesis doctoral en la UNAM
el dominicano estuvo aqui
pfff gracias
los amo
Cómo puede ser que indiquen que el dominio de todas las funciones trigonométricas es R, cuando es claro que por ejemplo en el caso de la tangente, no está definida para valores impares de Pi/2!!!!!!!!! Lo mismo con las inversas; no están definidas para todos los casos en que se anule el denominador!!!! (seno, coseno o tangente). Terrible!
Sí Adriana, la formulación general del dominio de todas las funciones trigonométricas no debe referirse en todos los casos a R.
Puedes consultar la formulación correcta y gracias.
Con R se refieren a un numero real, no especificado, pero que entra en los reales
Si
Excelente, me ayudo en mi tarea de preparatoria
Muchas gracias, me ha servido bastante.
Ojala existieran mas explicaciones asi. ! (y)
Excelente publicación me ayudo mucho con mi tarea de Universidad
me ayudo demasiado gracias
necesito cittar este docmento me puede ayudar
Porque no sale el rango?
Está el codominio. Rango o imagen es el codominio (o con un matiz, que para el caso no tiene repercusión). Pero recogemos tu sugerencia. Gracias, Eloisa.
Me parece excelente y bastante completo comparado con otros portales. La palabra » cateto» se puede usar tambien como «los lados del triangulo» y » cateto contiguo» como «lado adyacente», para que el lenguaje sea mas universal.
Gracias, Félix, por la sugerencia. Desconocíamos esa terminología. A los lados también se les denomina costados?. Puedes concretar la sugerencia? Te refieres al caso del triángulo rectángulo, el cual tendria tres catetos, dos de los cuales, los que forman el ángulo recto, serian catetos adyacentes?
Hola, Félix. No hemos encontrado en el uso del español que cateto pueda referirse en general a cualquier lado de un triángulo. A no ser que nos des alguna pista de algún uso local, catetos son los dos lados que forman el ángulo recto en un triángulo rectángulo. Tienes razón en que cateto adyacente tiene un uso más formal y generalizado, referido al cateto que, junto a la hipotenusa, forma uno de los ángulos agudos del triángulo rectángulo. Cateto contiguo, aunque más comprensible, es menos formal y, desde luego, lo tendremos en cuenta. Gracias otra vez.
Gracias me será de mucha ayuda para mi proyecto de matemáticas
Jajaja contingente xD
Excelente aportación.
Me gustan mucho las matemáticas, pero por alguna razón pensaba que son difíciles. Ahora sé que es cuestión de quitarse esa idea de la cabeza y estudiar.
Gracias
jsjsjjsjsjjsjs neta