
Un trapecio es un polígono con cuatro lados (cuadrilátero) siendo solo dos de sus lados paralelos y desiguales (las bases a y b).
Elementos y propiedades del trapecio
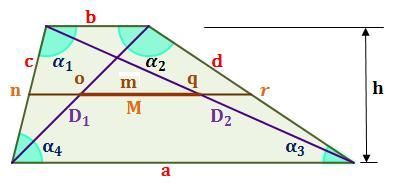
- Lados: un trapecio tiene cuatro lados (a, b, c y d), siendo dos paralelos (a y b) y los otros oblicuos (c y d).
- Bases: las bases del trapecio son los dos lados paralelos (a y b).
- Ángulos: tiene cuatro ángulos (α1, α2, α3 y α4). Los ángulos interiores, como en todo cuadrilátero, suman 360º (¿por qué suman 360º?), es decir, α1+α2+α3+α4=360º. Estos ángulos definen el tipo de trapecio que es.
- Altura (h): es la distancia entre las dos bases (a y b).
- Diagonales: las diagonales son segmentos que unen dos vértices no consecutivos. Tiene dos diagonales desiguales (D1 y D2), salvo en el caso del trapecio isósceles que son iguales.
Las fórmulas de las diagonales de un trapecio, conociendo sus cuatro lados son:

- Ejes de simetría: son líneas imaginarias que dividen el trapecio en dos partes simétricas respecto a dicho eje. Solamente tiene un eje de simetría el trapecio isósceles.
- Mediana (M): es un segmento paralelo a las bases (a y b) e intermedio a éstas. Su longitud se calcula como media de la longitud de las bases.
- Centroide (G): se encuentra a una distancia de la base mayor como indica la expresión:

Tipos de trapecio
Los trapecios se pueden clasificar en tres tipos según sus ángulos interiores.
- Trapecio rectángulo: tiene dos ángulos consecutivos rectos (de 90º). Por tanto, un lado es perpendicular a las bases.
- Trapecio isósceles: los ángulos son iguales dos a dos. Tiene dos lados oblicuos de igual longitud.
- Trapecio escaleno: los cuatro ángulos interiores son desiguales.

Área de un trapecio
El área del trapecio se calcula a partir de su altura y los dos lados paralelos (a y b) o bases del trapecio. Es el resultado de multiplicar su altura (h) y la mediana del trapecio, que se obtiene como la media de las dos bases a y b: M=(a+b)/2.


También se puede hallar el área de un trapecio conociendo sus cuatro lados.
O bien aplicando la fórmula:

O también mediante el segundo procedimiento que se describe entrando en el área del trapecio.
El área del trapecio se puede obtener con las longitudes de sus diagonales y el ángulo que forman.

Así, la formula es:

Donde los senos de los ángulos ε y θ son iguales por ser ángulos suplementarios.

Un caso particular es cuando el ángulo que forman las diagonales del trapecio es un ángulo recto de seno igual a 1:
Y la fórmula del área queda simplificada a la de todo cuadrilátero cuyas diagonales sean perpendiculares:

Altura del trapecio
La altura de un trapecio se puede hallar, conociendo sus cuatro lados, siendo a la base mayor y b la menor, mediante la fórmula:

Perímetro del trapecio

El trapecio puede tener sus cuatro lados desiguales, por lo que su perímetro es la suma de los cuatro lados.


En el caso particular del trapecio isósceles, los lados oblicuos (c) son iguales. Por lo tanto, su perímetro será la suma de las bases más el doble del lado oblicuo (c).


Puede hallarse también el perímetro de un trapecio rectángulo en función los lados a, b y c.
Mediante el teorema de Pitágoras:
Trapecio inscrito a una circunferencia
Solamente pueden inscribirse a una circunferencia los trapecios isósceles.

Trapecio circunscrito a una circunferencia
Para que un trapecio pueda circunscribirse a una circunferencia debe cumplirse la condición de que la suma de las longitudes de los lados paralelos (o bases) debe ser igual a la suma de las longitudes de los lados oblicuos:
El radio de la circunferencia inscrita es la mitad de la altura del trapecio:

Válido para los tres tipos de trapecios.
Diagonales de un trapecio

La longitud de las diagonales del trapecio se pueden calcular mediante esta fórmula, a partir de la longitud de los cuatro lados del trapecio:

Las dos diagonales de cualquier trapecio también cumplen la siguiente relación con sus cuatro lados. Esta relación se deduce de las dos fórmulas anteriores:

El segmento interior TV de un trapecio, paralelo a sus bases que pasa por el punto de intersección de sus diagonales U.
Queda dividido en dos subsegmentos iguales TU y UV, de longitud:

Y el segmento JL, que une los puntos medios de las bases, pasa por el punto K de la intersección de las diagonales. Los subsegmentos JK y KL son las medianas de dos triángulos semejantes opuestos por el vértice K y formados por los subsegmentos de las diagonales y las bases del trapecio.

Mediana de un trapecio
La mediana de un trapecio M es un segmento paralelo a sus bases situado a la mitad de su altura. Une los puntos medios de los lados oblicuos c y d.
Por el primer teorema de Tales, la mediana M corta a las dos diagonales D1 y D2 por sus puntos medios.
Su longitud, en función de sus bases, es:

Con las diagonales del trapecio se forman unos segmentos que cumplen las siguientes propiedades:

- Segmento m de la mediana comprendido entre sus intersecciones con las diagonales:

- Segmentos comprendidos entre un extremo de la mediana y su diagonal más próxima:

- Segmentos comprendidos entre un extremo de la mediana y la diagonal más alejada:

Centroide del trapecio
Para determinar el centroide de un trapecio utilizamos un procedimiento gráfico como el que indica la figura:

Se prolonga en un sentido la base mayor a en una longitud igual al de la base menor b (punto M).
Se prolonga en el sentido contrario la base menor b en una longitud igual al de la base mayor a (punto N).
Trazamos la recta MN.
Trazamos el segmento que une los puntos medios de ambas bases (ab).
En la intersección de ambos segmentos se encuentra el centroide G del trapecio.
El centroide G se encuentra a una distancia de la base mayor de:

Construcción de un trapecio

Construcción geométrica de un trapecio cualquiera, a partir de sus cuatro lados.
- Trazar el segmento de la base mayor a (QN).
- Sobre ella, marcar la longitud de la base menor b (QM).
- Con centro en M trazar un arco de radio c.
- Con centro en N trazar un arco de radio d.
- Estos dos arcos se cortan en el punto O.
- Con centro en Q trazar un arco de radio c.
- Con centro en O trazar un arco de radio b.
- Estos dos arcos se cortan en el punto P.
- Uniendo Q,N,O,P,Q queda construido el trapecio.
Obsérvese que Q, M, O, P, Q es un paralelogramo, con cuatro lados, siendo iguales y paralelos dos a dos. Por lo tanto las bases a y b son paralelas. En consecuencia, hemos construido un trapecio.
Ejercicios
Ejercicio 1

Hallar el área de un trapecio de 7 cm y 3 cm de bases y 4 cm de altura.
Solución:
Aplicamos la fórmula general del àrea del trapecio:

Ejercicio 2

Hallar el área de un trapecio cuyas bases miden 7 cm y 3 cm y sus lados oblicuos 5 cm y 4,12 cm. Calcular la longitud de sus diagonales.
Solución:
Se aplica, en primer lugar, la ecuación del área del trapecio, cuando se conocen sus cuatro lados:

Ahora vamos a averiguar las diagonales:

Mediante las fórmulas que depende también de los lados:

Y aplicamos los valores de los cuatro lados.
En primer lugar se halla la diagonal D1:

Después calcularemos la longitud de la diagonal D2:

Ejercicio 3

Determinar si se puede circunscribir o inscribir una circunferencia al trapecio de los ejercicios 1 y 2, cuyas bases miden 7 cm y 3 cm y sus lados oblicuos 5 cm y 4,12 cm.
Solución:
A la primera cuestión: sus lados oblícuos no son iguales. Por lo tanto no es un trapecio isòsceles. La respuesta es que no se le puede circunscribir una circunferencia.

Ahora contestamos a la segunda pregunta. Debemos comprobar la condición de los trapecios inscritos a una circunferencia, o, lo que es lo mismo, circunscribir una circunferencia a un trapecio. La suma de las bases debe de ser igual a la suma de los lados oblícuos:
Si le aplicamos los valores de los lados a la condición:

Vemos que tampoco se puede inscribir una circunferencia a este trapecio.

Ejercicio 4

Hallar el área de un trapecio cuyas diagonales miden 6,71 cm y 4,24 cm. Las diagonales forman entre sí un ángulo de 75,57°.
Solución:
Mediante la fórmula del área por las diagonales y su ángulo, se le aplican los valores y:

Con lo que el área tendrá 13,5 cm2.
Ejercicio 5

Hallar la relación entre las bases de un trapecio en el que sus diagonales dividan a la mediana en tres segmentos iguales.
El planteamiento dice que las dos diagonales D1 y D2 dividen a la mediana M en tres segmentos iguales, tales que:
NO = OQ = QR
En las relaciones de los segmentos de la mediana de un trapecio que forman las diagonales hemos visto arriba que el segmento m = OQ es igual a:

Pero que también, que los segmentos exteriores de la mediana, NO y QR son iguales entre sí e iguales a la mitad de la base superior:

Al ser los tres segmentos iguales, igualamos sus expresiones equivalentes:

Solamente nos queda eliminar los denominadores multiplicando en cruz y simplificar:

Por lo tanto, todo trapecio en el que sus diagonales dividan a la mediana en tres segmentos iguales, la base inferior será el doble que la base superior.




Hola soy Génesis curso sexto de primaria y busco la dos fórmulas y resultado de área y perímetro de un trapecio rectangular
Puedes ver las fórmulas directamente en la página Trapecio rectángulo de UNIVERSO FÓRMULAS.
Si el perímetro lo quieres en función de los lados a, b y c, mira el triángulo rectángulo que se forma en el ejercicio:
P = a + b + c +√[c² + (a – b)²]
no dejaron la formula para obtener el centroide del trapecio en el eje x pero es la siguiente formula X=(1/3)*((a^2+a*b+b^2)/(a+b))
Freddy, en esta página tienes la fórmula de la distancia del centroide del trapecio a la base mayor. Si el trapecio lo ubicas en un sistema de referencia, tal que la base mayor esté en el eje X, la fórmula de esta página sería la ordenada del centroide del trapecio.
Revisa tu fórmula.
hola estoy en primaria y me da mucha curiosidad que me expliquen que es el teorema de Pitagoras😕
Consulta Teorema de Pitágoras en UNIVERSO FÓRMULAS
Hola, tengo un ejercicio por resolver «Demuestre que la recta que une los puntos medios de los lados paralelos de un trapecio pasa por el punto de intersección de las diagonales» ¿me pueden ayudar?
Para no desarrollar la demostración. Los dos triángulos formados por las diagonales y las bases son semejantes. Ángulos opuestos iguales. La recta que une los puntos medios de las bases son las medianas de esos dos triángulos semejantes. Juntas forman el segmento que unen los puntos medios de las bases.
nop
les falta poner los volumenes de las figuras geometricas
Consulta las fórmulas del volumen de los distintos tipos de cuerpos geométricos: de poliedros (regulares, irregulares, como prismas, pirámides) o cuerpos de revolución en UNIVERSO FÓRMULAS. Encontrarás lo que buscas
Me podrían ayudar con este ejerció.
El segmento interior de la paralela a las bases de un trapecio por el punto de intersección de las diagonales es bisecado por dicho punto. Demostrar dicha proposición y calcular la longitud de tal segmento en función de las bases
La demostración geométrica rebasa esta contestación.
Efectivamente el segmento interior paralelo a las bases es dividido en dos iguales (bisectado) en el punto de intersección de las diagonales.
La longitud de cada uno de estos dos semisegmentos es = (a * b) / (a + b)
a y b son las bases (dibujo)
ayudenme si en un trapecio ABCD en donde PQ es una base media BC es base menor y AD es base mayor y PQ=17 y MN= 3 y CQ=QD y PB=AP como se halla la base mayor AD.
Mira las fórmulas de esta página
M = NR = (a + b) / 2 = 17 (NR sería tu mediana de 17)
m = OQ = (a – b) / 2 = 3 (OQ supongo que será tu segmento MN = 3)
Resuelves este sistema de dos ecuaciones de primer grado con dos incógnitas y tienes la base mayor AD = a = 29,14
me podrian resolver este problema en un trapecio ABCD BC base menor la medida del angulo A =60 y la medida del angulo D =20 si BC =& calcular la mediana del trapecio
Qué quieres decir con que BC = &
buenas noches tengo una tarea de mi hijo q cursa septimo grado si me pudieran hacer el favor y colaborarme con este.
ejercicio : se tiene un trapecio con base 1=4,5 cm , base 2=5,5 cm y altura h= 4 cm , dentro de el hay un circulo con una circunferencia (perimetro) de 12,56 cm.
a. Hacer el dibujo.
b. Determina el area de la superficie que esta fuera del circulo pero dentro del trapecio.
Les agradezco y mil gracias, espero su respuesta.
Averiguar el radio de ese círculo.
Perímetro = 2 * π * r
12,56 = 2 * π * r
r = 2 cm
Como la altura del trapecio es de 4 cm, el círculo es tangente a las bases, porque la altura y el diámetro coinciden.
Como el diámetro paralelo a las bases es menor que las dos, el círculo no llega a los lados laterales.
El área del círculo = π * r² = 12,56 cm²
Área del trapecio = 4 * (5,5 + 4,5) / 2 = 20 cm²
Diferencia de áreas:
20 – 12,56 = 7,53 cm²
Dibuje un trapecio con esas medidas, por ejemplo un trapecio rectángulo y trace una circunferencia de radio 2, tangente a las bases y al lado lateral perpendicular.
Hola no se que es un octógono
es encerio :v
🤣🤣🤣🤣🤣
Una pregunta se trata de un ejercicio donde me dice lo siguiente:
En un trapecio ABCD (AB//CD). Si m < B=2*m <D. AB=5 y BC=12. Entonces el valor de CD es…
He intentado varias veces y no puedo resolverlo
No capto lo de «m < B=2*m < D»
Supongo que m será la mediana.
en mediana corta es menos
Jean, a qué te refieres con «mediana corta»? Gracias.
Si es al segmento m, la fórmula que figura és m = (a – b) / 2
me pueden decir que angulos tienen los triangulos
gracias buena pagina
Hola no se q es el centroide…. alguien puede explicarme…?
El centroide es el centro de masas (o centro de gravedad) de una figura geométrica, sea lineal, superficie o un cuerpo geométrico.
I es que las figuras geométricas, de carácter abstracto, tienen densidad uniforme.
En pocos dias aparecerá en Universso Fórmulas una página para el centroide, centro de masas,baricentro o centro de gravedad, conceptos de sentido muy próximo.
De momento, visita la página de Universo Fórmulas «Centroide de un trapecio».
Muy cool me sirvio de mucho
Estupendo
Hola muy buena pagina megustaria agregarme como lo ago.ayuda
Gracias me sirvió mucho
toda esta pajina me a ayudado en mi tarea gracias a los creadores de este foro asi que muchas gracias
Yo no entiendo nada y me tengo que aprender todas las fórmulas y no me las se
estupendo!!!
quiero q me enseñen mis tareas de matematica
porfavor es de las formulas de trapecio
Que buena página. Sigan así.
Gracias en serio me fue muy útil me saqué un 10
FANTASTICO.
YO.ME GUSTA PERO LO REPROBE MI EXAMEN.AUN NO LO ENTENDI.
que increible y asi es mas facil antes no sabia ahora gracias a eso ya se pero un poca mas muchas grasias por escucharme espero que sigan explicando mas fasil
Gracias por tu ayuda
de nada amigo