
Un rombo es un polígono con cuatro lados (cuadrilátero) siendo los cuatro iguales. Tiene cuatro ángulos interiores iguales dos a dos.
Elementos y propiedades del rombo

- Lados: el rombo tiene cuatro lados (a) iguales.
- Ángulos: tiene cuatro ángulos (dos α y dos β) iguales dos a dos. Los ángulos interiores, como en todo cuadrilátero, suman 360º (2π radianes).
- Diagonales: las diagonales son segmentos que unen los vértices no consecutivos. Tiene dos diagonales (D y d) desiguales y perpendiculares. Se cortan en el centro del rombo. Las diagonales son las bisectrices de los ángulos. También son ejes de simetría.
- Ejes de simetría: son líneas imaginarias que dividen el rombo en dos partes simétricas respecto a dicho eje. Tiene dos ejes de simetría (E1, E2) que coinciden con las diagonales.
Un caso particular de rombo es el cuadrado, donde todos los ángulos son iguales (es decir, (α=β). Los ángulos serán todos rectos (de 90º) y las diagonales iguales.
Diagonales del rombo

El rombo tiene dos diagonales (D y d) perpendiculares y que se cortan en el centro del rombo. D es la diagonal mayor y d la diagonal menor.
Existe una fórmula que relaciona las diagonales del rombo y uno de sus lados (a). La relación es la siguiente:

Ésta fórmula se obtiene directamente de la llamada ley del paralelogramo.
También podría obtenerse también a partir del teorema de Pitágoras, ya que la mitad de cada una de las diagonales (D/2 y d/2) y un lado del rombo forman un triángulo rectángulo.

Área del rombo
Existen varias fórmulas para calcular el área del rombo. La más común es mediante las dos diagonales del rombo (las diagonales de un rombo son perpendiculares). El área es la mitad del producto de las diagonales (D y d).



Otra forma de calcular el área del rombo es mediante la fórmula del área del paralelogramo. En este caso, un lado (a) se considera la base del rombo. Se mide la altura (h) relativa a dicha base, de manera que el área será el producto de la base por la altura.


Y una tercera fórmula se obtiene a partir del lado y un ángulo:
Perímetro del rombo

El perímetro de un rombo podemos hallarlo por sus lados o por sus diagonales.
El perímetro es cuatro veces la longitud de uno de sus lados (a), ya que tiene sus cuatro lados iguales.

Igualmente podemos calcular su perímetro si conocemos las diagonales de un rombo D y d.

Se forman cuatro triángulos rectángulos iguales en los que los catetos son la mitad de las diagonales (D/2 y d/2). El lado a será su hipotenusa. Podemos aplicar, por lo tanto, el teorema de Pitágoras:
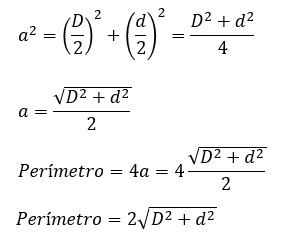
Con lo que tenemos la fórmula del perímetro a partir de las diagonales de un rombo.
Ejercicios
Ejercicio 1
Sea un rombo que se conoce la longitud de sus dos diagonales (D y d), siendo la diagonal mayor D=5 cm y la diagonal menor d=3 cm.
Su área será un medio por el producto de las diagonales, es decir:

Por lo tanto, el área de éste con diagonales de D = 5 cm y d = 3 cm es de 7,5 cm2.
Ejercicio 2
Hallar el área de un rombo de lado 5 cm y en el que sus ángulos menores miden 73,74°.
Solución:
Ejercicio 3

Sea un rombo cuyos lados son todos iguales y de longitud a = 5 cm.
Su perímetro será cuatro veces la longitud de su lado, es decir:
Y se obtiene que el perímetro de éste con lados de 5 cm es de 20 cm.

muy exelente de verdad
de nada yolo
Hola, cómo puedo encontrar la región sombreada de un cuadrado que mide 6X6 y arriba de este se forma una figura sin ángulos pero supongamos que es un rombo. Y me da el dato de que de la punta del supuesto rombo hacia abajo del cuadrado mide 10 u.
hola, como hago para determinar las vertices, angulos interiores y exteriores, y 2 diaginales de un rombo si solo se que es un poligono rombo ABCD.?
Hola para obtener los ángulos de un rombo que miden 10 cm por lado, como puedo sacarlo?
Falta un dato ( p.e. una diagonal o el área).
Hay infinitos rombos de lado 10 cm.
Necesito ayuda, el problema dice: halla los ángulos internos del rombo sabiendo la diagonal mayor (D) 24 cm y uno de sus lados 15 cm.
Fíjate en la primera figura de la página. El rombo está dividido en cuatro triángulos rectángulos de hipotenusa 15 cm y cateto mayor 24/2 = 12 cm.
Por trigonometría:
cos (α / 2) = 12 / 15
sen (β / 2) = 12 / 15
Halla el arcoseno y el arcocoseno correspondiente para saber los ángulos que buscas.
α = 73,74°
β = 106,26°
Resuelve y comprueba
Cual es la fórmula de un rombo?
Las fórmulas del rombo las tienes aquí
como hallar el lado de un rombo?
En esta misma página están las fórmulas para hallar los lados a partir de las diagonales, del perímetro …
Disculpa, como puedo obtener el área si tengo solo la.medida del perímetro?
El lado es
a = p / 4
Pueden haber muchos rombos diferentes con el mismo lado.
Sin solución. Faltan datos
hola como hago para haberiguar el perímetro de un rombo sabiendo sólo la medida de una de las diagonales?
No se puede.
Solicito apoyo para este Calcular el Perimetro de un rombo cuya diagonal menor mide 12 cm y un ángulo interior mide 60
Está la solución trigonométrica tomando 30° como el ángulo que forma un lado con la diagonal mayor, que es la bisectriz. Con el coseno de 30° y media diagonal 12/2 sacarías el lado.
Pero, ¿que te parece atajar?
Si el ángulo es de 60°, entonces los dos triángulos con que divide la diagonal menor al rombo son equiláteros, con lo que el lado también es 12 y el perímetro 12*4 = 48 cm.
Que es un rombo? 🤔
Definición de rombo. … Como el rombo cuenta con cuatro lados, se lo califica como cuadrilátero. Por otra parte, dentro del grupo de los cuadriláteros, el rombo es un paralelogramo, ya que dispone de lados paralelos (dos a dos) y con lados opuestos que son iguales.
el
Exacto, Álex, como se indica en esta página.
Además, los cuatro lados también son iguales.
Cuanto mide los angulos de un rombo?
Total 360°
Iguales dos a dos, los opuestos
Necesito ayuda, el problema dice: halla el perímetro de un rombo cuyas diagonales miden 6 y 4 cm
Tienes la fórmula justo en esta misma página:
4a² = D² + d²
Y perímetro = 4a
Dale valores y resuelve.
Quiero hacer, los pisos de las iglesias antiguas, llevan 3 rombos que conforman un cubo en 3 D.
de que medidas deberían ser a modo de ejemplo. ¿es un rombo ?
Por si te sirve, consulta el desarrollo de un romboedro en la página tipos de paralelepípedos en UNIVERSO FORMULAS.
Una pregunta cual es la formula del rombo ?
En esta misma página tienes la fórmula de la relación entre los lados y las diagonales, dos fórmulas para hallar el área y la del perímetro.
Quien me puede ayudar, necesito saber q matemático trabajo con el rombo
como puedo resolver este problema que dice :el perimetro de un rombo mide60dm y sus diagonalesentresicomo 3 es a 4
a = Perímetro / 4 = 60 / 4 = 15 cm
d/D = 3/4
d = 3D/4
Teorema de Pitágoras a uno de los cuatro triángulos rectángulos que forman las dos diagonales, donde la hipotenusa es el lado a
(D/2)² + (3D/8)² = 15²
Despejas D.
Luego hallas d (d = 3D/4)
El área = D*d/2
me ayudo
mejor que wikipedia
Gracias, Anonimus.
gracias por todoooo mijas
Si muchas gracias me ayudaron con mi tarea??
sabe sipre estaremos para ayudarle
excelente pagina