
El teorema de Euler para poliedros establece una relación entre los números de caras (C), aristas (A) y vértices (V) que se cumple para todo poliedro convexo. La relación es la siguiente:

Ejercicio
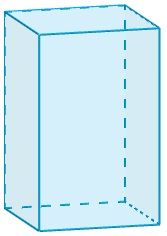
Supongamos que tenemos un prisma cuadrangular.
Éste tiene seis caras, C=6, las dos bases y los cuatro paralelogramos de los laterales. También es conocido el número de vértices que tiene, V=8.
¿Cúantas aristas (A) tiene el prisma cuadrangular?
Y se obtiene que tiene doce aristas, A=12.

De nascar
este man
es un jeeeefe el q lo izo.
se te quiere jajjajjajj
mandame algo que tengas de sistemas ejes cristalograficos prismas hexgono triangular triclinico
Buen trabajo
y dela piramide cuantas aristas hay
Se cumple para todos los poliedros, incluido las pirámides
Muy bién Zaidy. También para las pirámides (que son poliedros), siempre que éstas sean convexas.
Buenos consejos, y interesante teoria. Bien hecho señor Euler