Operaciones con fracciones

Las operaciones con fracciones más importantes son:

• Suma de fracciones
• Resta de fracciones
• Multiplicación de fracciones
• División de fracciones
• Potencia de fracciones

Hay que tener en cuenta si los denominadores de las fracciones son iguales o diferentes, ya que esto podrá cambiar el método para realizar la operación.

Suma de fracciones

Cuando queremos realizar la suma de fracciones se pueden dar dos casos:

• Las fracciones que se suman tienen el mismo denominador (fracciones homogéneas). Por ejemplo:
  
• Las fracciones que queremos sumar tienen diferente denominador (fracciones heterogéneas). Por ejemplo:
  

¿Cómo se suman las fracciones? Según el caso en el que estemos, el procedimiento para realizar la suma es diferente. Vamos a ver los dos casos.

Suma de fracciones con el mismo denominador

Para la suma de fracciones con igual denominador (también llamadas fracciones homogéneas), se suman los numeradores y se deja el mismo denominador.

Por ejemplo:

En este caso, como el denominador es igual, o sea 6, sumamos los dos numeradores 1 y 2.

Por lo tanto, el numerador será 3 y el denominador lo dejamos igual, siendo 6.

Este procedimiento es muy sencillo, ¿verdad?

Suma de fracciones con diferente denominador

¿Cómo sumar fracciones con diferente denominador? Se puede hacer por dos métodos, el método del mínimo común denominador para la suma de dos o más fracciones y el método de la multiplicación en cruz para la suma de dos fracciones. El método más utilizado el el del mínimo común denominador.

Método del mínimo común múltiplo de los denominadores

Lo primero que debemos hacer para sumar fracciones con distinto denominador, es encontrar un denominador común. Para ello, debemos encontrar el mínimo común múltiplo de los denominadores de las fracciones que sumamos. Veámoslo en un ejemplo.

Supongamos que queremos sumar:

Como las fracciones tienen diferente denominador, necesitamos ponerlas todas en uno mismo. Para ello, hacemos el mínimo común denominador, es decir, el mínimo común múltiplo de los dos denominadores.

1. Primero factorizamos los dos denominadores: 4 y 3 en factores primos.
   
2. Con la factorización hecha, sacamos el mínimo común múltiplo (mcm) de 4 y 3. Recordamos que el mcm, una vez hecha la factorización, son los factores comunes y no comunes elevados al máximo exponente. En nuestro caso será:
   
3. El mínimo común múltiplo de los denominadores es 12. Los denominadores de las nuevas fracciones serán 12 y los numeradores serán el numerador original por 12 dividido entre el denominador original, es decir:
   
4. Ahora tenemos las dos fracciones con el mismo denominador. Podemos hacer la suma de éstas, poniendo en el numerador la suma de los numeradores (3+8=11) y dejando el denominador en 12.
   

Así conseguimos realizar la suma de fracciones con distinto denominador, que es un poco más complicado que sumar fracciones con igual denominador.

Método de la multiplicación en cruz

El método de la multiplicación en cruz sirve para sumar dos fracciones. En este caso, si las fracciones que se suman tienen los mismos denominadores, se pueden sumar por el método normal de la suma de fracciones con el mismo denominador.

En el caso de que las fracciones tengan diferentes denominadores, es cuando podemos utilizar el método de la multiplicación en cruz.

1. Imaginemos que queremos sumar las siguientes fracciones:
   
2. Para calcular el numerador de la fracción resultado, multiplicamos las fracciones en cruz, es decir, el numerador de la primera por el denominador de la segunda y el denominador de la primera por el numerador de la segunda, y sumamos las dos multiplicaciones.
   
3. El denominador de la fracción resultado será el producto de los dos denominadores: 7 · 5 = 35.
4. Por lo tanto, el resultado de la suma de estas fracciones será 31/35.
   

Resta de fracciones

Cuando se realiza la resta de fracciones, se pueden dar dos casos:

• Las fracciones que se restan tienen el mismo denominador (fracciones homogéneas). Por ejemplo:
  
• Las fracciones que se desean restar tienen diferente denominador (fracciones heterogéneas). Por ejemplo:
  

¿Cómo se restan las fracciones? Según los dos casos anteriores, que los denominadores sean iguales o diferentes, utilizaremos uno de los siguientes métodos. Veamos los dos casos.

Resta de fracciones con el mismo denominador

Para la resta de fracciones con igual denominador (también llamadas fracciones homogéneas), se restan los numeradores y se deja tal cual el denominador.

Por ejemplo:

En este ejemplo, como el denominador es igual en las dos fracciones, o sea 5, restamos el primer numerador menos el segundo, 6 y 2.

El numeradores será 4 y el denominador, como habíamos dicho se quedaba igual, siendo 5.

Resta de fracciones con diferente denominador

¿Cómo se restan dos fracciones que tienen diferente denominador (también llamadas fracciones heterogéneas)? Para realizar la resta, se pueden emplear dos métodos, el método del mínimo común denominador y el método de la multiplicación en cruz. El método más utilizado el el del mínimo común denominador.

Método del mínimo común múltiplo de los denominadores

En el método del mínimo común múltiplo de los denominadores, o del mínimo común denominador, lo primero que haremos para restar fracciones con distinto denominador es encontrar el denominador común. Para encontrarlo, calcularemos el mínimo común múltiplo de los denominadores de las fracciones que deseamos restar. Vamos a verlo en un ejemplo.

Supongamos que queremos restar:

Como las fracciones tienen diferente denominador, lo primero que debemos hacer es pasarlas al mismo. Para ello, hacemos el mínimo común denominador, es decir, el mínimo común múltiplo de los dos denominadores.

1. Se factorizan los dos denominadores, 4 y 10 en factores primos.
   
2. Una vez está la factorización, obtenemos el mínimo común múltiplo (mcm) de 4 y 10. Recordamos que el mcm, una vez hecha la factorización, son los factores comunes y no comunes elevados al máximo exponente. Veamos que da en nuestro caso:
   
3. El mínimo común múltiplo de los denominadores es 20, por lo tanto, los denominadores de las dos nuevas fracciones serán 20. Los numeradores nuevos serán el numerador original por 20 dividido entre el denominador original, es decir:
   
4. Ahora que tenemos las dos fracciones con el mismo denominador, se puede hacer la resta de éstas, poniendo en el numerador la resta de los numeradores nuevos (15-4=11) y dejando el denominador en 20.
   

Al final logramos realizar la resta de fracciones con distinto denominador, que es un poco más complicado que restar fracciones con igual denominador.

Método de la multiplicación en cruz

El método de la multiplicación en cruz se utiliza para restar dos sirve para sumar dos fracciones con distinto denominadores.

Este método puede resultar más fácil que el método mínimo común denominador, ya que te ahorras calcular el mínimo común múltiplo (mcm) de los denominadores. Sin embargo, por el otro método obtendrás, en la mayoría de los casos, como resultado una fracción más simplificada.

1. Vamos a ver como funciona este método en el siguiente ejemplo:
   
2. El numerador de la fracción resultado, se multiplican las fracciones en cruz, el numerador de la primera por el denominador de la segunda se le resta el producto del denominador de la primera fracción por el numerador de la segunda.
   
3. El denominador de la fracción resultado será el producto de los dos denominadores: 5 · 7 = 35.
4. Es decir, el resultado de la resta de estas fracciones será 16/35.
   

Multiplicación de fracciones

La multiplicación de fracciones representa la parte de una parte. Veámoslo en un ejemplo:

Carla y Daniela se van a comer una pizza. Daniela corta la pizza en 6 trozos iguales. Carla tiene hambre y le apetece un trozo, pero como los trozos que hay le parecen demasiado grandes, decide cortar uno de los trozos por la mitad.

El trozo que cogerá Carla será un doceavo (1/12) y se obtiene como el producto de dos fracciones.

Como multiplicar fracciones

El resultado del producto de dos fracciones es otra fracción.

El numerador es el producto de los numeradores y el denominador el de los denominadores:

¿Cómo se multiplican las fracciones? El producto de fracciones es muy sencillo, tan solo ha que seguir los pasos siguientes:

1. El numerador de la fracción resultado (el número de arriba) será el producto de los numeradores (el producto de los números de arriba de las fracciones).
   
2. El denominador del resultado (el número de abajo) será el producto de los denominadores (los números de abajo de las fracciones que se multiplican).
   
3. Una vez tenemos el número de arriba y abajo de la fracción, debemos simplificar la fracción.
   

División de fracciones

La división de fracciones, como concepto, es la parte de una parte. Se aprecia mejor en un ejemplo:

Nos queda la mitad (1/2) de una pizza. Queremos darle a cada uno de nuestros invitados una porción de pizza que corresponde a un sexto de pizza (1/6). El número de invitados a los que les podremos dar una porción de pizza se obtiene dividiendo el total de la pizza, 1/2, por la fracción 1/6.

Como dividir fracciones

El resultado del cociente de dos fracciones es otra fracción.

La división de dos fracciones es el producto de la primera por la inversa de la segunda. Más fácil, el cociente de dos fracciones se obtiene multiplicando «en cruz» las dos fracciones.

Vamos a verlo en un ejemplo. Suponemos que queremos hacer la siguiente división:

1. El numerador de la fracción resultado (el número de arriba) será el producto del numerador de la primera fracción y el denominador de la segunda. Es decir 2 · 6 = 12.
   
2. El denominador del resultado (el número de abajo) será el producto del denominador de la primera fracción por el numerador de la segunda fracción. Tendremos que 3 · 1 = 3.
   
3. Una vez tenemos el número de arriba (numerador) y abajo (denominador) de la fracción, debemos simplificar la fracción.
   

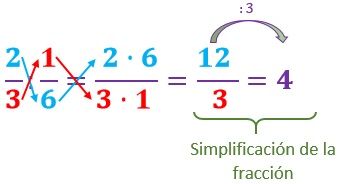
   Obtenemos que el resultado es 4.

Potencia de una fracción

Como sabemos por definición de potencia n, la potencia de una fracción es la multiplicación de esta fracción por sigo mismo n veces.

Esto acaba siendo lo mismo que elevar el numerador y el denominador a dicha potencia n.

Esta fórmula se utiliza cuando el exponente (el número n) sea un número entero y positivo. Lo normal será este caso, pero suponiendo que el exponente sea entero, se pueden dar tres casos.

1. Exponente entero positivo.
2. Exponente cero.
3. Exponente entero negativo.

El primer caso ya lo hemos visto. Vamos a hacer ahora un ejercicio:

Ejercicio

Resuelve la potencia de la fracción 5/2 elevada al exponente 3.

El numerador resultado será numerador elevado a 3 (5³ = 125) y el denominador será 2³ = 8.

Potencia con exponente cero

Toda potencia con exponente cero es igual a la unidad. Por lo tanto, la potencia de cualquier fracción con exponente 0 es igual a 1.

Potencia con exponente negativo

Cuando el exponente es un número entero negativo, al igual que cuando el exponente es cero, la definición del inicio de la potenciación carece de sentido, ya que no tiene lógica multiplicar un número por sí mismo un número negativo de veces.

Una fracción elevada a un número entero negativo es la fracción invertida (es decir, el numerador pasa a ser el denominador y el denominador el numerador) elevada al exponente en positivo.

Vamos a verlo en un ejemplo. Suponemos que queremos resolver la siguiente potencia, con el exponente -2, un número entero negativo:

Intercambiamos el numerador por el denominador y lo elevamos a 2.

Obtenemos que el resultado será 9/4.