
El movimiento circular uniforme (MCU) es el movimiento que describe una partícula cuando da vueltas sobre un eje estando siempre a la misma distancia (r) del mismo y desplazándose a una velocidad constante.
Posición
La posición de la partícula depende de su posición inicial y de la velocidad a la que se desplaza. Ésta se puede calcular a partir del incremento angular, de la velocidad angular y de la velocidad tangencial (en caso de conocer las velocidades es necesario saber el tiempo t que se ha movido el cuerpo o partícula).
Posición según el incremento del ángulo
Podemos calcular la posición de la partícula a partir del incremento del ángulo:
En coordenadas cartesianas tenemos:


Relación entre el incremento angular y la longitud del arco recorrido
La relación entre el incremento angular y la longitud de arco de circunferencia recorrido se puede expresar con la fórmula de la figura:

(Ángulo theta en radianes).
Posición según la velocidad angular
La posición de la partícula se puede calcular a partir de la velocidad angular y el tiempo
En coordenadas cartesianas tenemos:


Posición según la velocidad tangencial
También se puede calcular la posición de la partícula a partir de la velocidad tangencial
En coordenadas cartesianas tenemos:
Nota: Las unidades del ángulo son siempre en radianes.
Velocidad angular
En el MCU, la velocidad angular se puede calcular a partir del período o la frecuencia, ya que el período y la frecuencia son constantes.
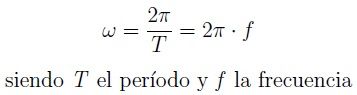
Otra forma de determinar la velocidad angular es:

Las unidades en las que se mide la velocidad angular ω es en radianes/seg, o simplemente en s-1.
La velocidad angular en el MCU es constante.
Velocidad tangencial
La velocidad tangencial es igual a la velocidad angular por el radio.

La velocidad tangencial, al igual que la velocidad angular, en el MCU es constante.
Aceleración centrípeta
A diferencia del movimiento rectilíneo uniforme, una partícula en un movimiento circular uniforme (MCU) si que tiene aceleración, la aceleración centrípeta. Esto se debe a que, aunque el módulo de la velocidad se mantiene constante, el vector cambia constantemente de dirección. Ésta se calcula como:


Aceleración angular y tangencial
En el movimiento circular uniforme (MCU), tanto la aceleración angular como la aceleración tangenciales son cero.
Período
La velocidad angular en el MCU es constante, por lo que el período también será constante e irá definido por la fórmula siguiente:

Frecuencia
La frecuencia es constante al ser constante la velocidad angular y el período:

Ejercicio
Una rueda gira a una velocidad constante de 120 revoluciones por minuto (r.p.m.). Hallar:
- La frecuencia en ciclos/segundo.
- La velocidad angular en radianes/segundo.
- La velocidad tangencial en un punto de la rueda situado a 15 cm. del eje.
- Las aceleraciones tangenciales y centrípetas en el punto citado.
Solución:
- La frecuencia en ciclos/segundo se calcula dividiendo las r.p.m. entre los 60 segundos que tiene un minuto:

- La velocidad angular (ω):

- La velocidad tangencial en un punto de la rueda situado a 15 cm del eje, el radio de rotación será de r=15 cm, por lo tanto:

- La aceleración tangencial es 0:

La aceleración centrípeta en el punto citado es:


Hola para todos!
excelente material!!
Me podrán ayudar a resolver el siguiente ejercicio??
la rapidez angular de una rueda es de 5rad/s y la rapidez circunferencial del borde es de 10m/s. Calcular el radio de la rueda
Es válido si transformo los datos de cm a m?
Por cierto, ¡excelente contenido!
Sí, si lo haces en todas las magnitudes
hola disculpa me puedes ayudar con un problema de movimiento circular uniforme or favor.
Una partícula parte del reposo del punto C en sentido antihorario con una aceleración tangencial 3m/s2 y gira un ángulo de 270o en una trayectoria circular de 2m de radio. Determinar:
a. La aceleración angular
b. La velocidad angular final
c. El tiempo empleado
d. La posición angular inicial y final
e. La rapidez final
Estás en un MCUA. Ves a esa página de UNIVERSO FÓRMULAS
Ahí encontrarás las fórmulas que buscas.
Se supone que el punto C es el de θ0 = 0°. Si gira alrededor del origen de coordenadas (0, 0) las coordenadas en C serán (2, 0)
a. α = at / r = 3 / 2 = 1,5 rad/s²
b. 3,76 rad/s
c. 2,5 s
d. Inicial 0° y (2,0). Final 270° y (0, -2)
e. 7,5 m/s
Anímate a aplicar las ecuaciones
hola me puedes ayudar con este problema
un cuerpo rota con movimiento circular uniforme alrededor de un punto con radio igual a 6 metros, si el cuerpo rota con una velocidad angular igual 0,65 metros/segundos
No está la pregunta y 0,65 m/s no es una velocidad angular ω.
Mira en la página MCU de UNIVERSO FÓRMULAS. Quizás estés buscando la velocidad angular.
v = ω r
tienen una calculadora para resolver estos ejercicios y que muestren los pasos?
En un columpio grande el asiento de una niña gira en una circunferencia de radio 7,4 m y angulo de 53ºformado por la vertical y por la cuerda que sostiene a la niña. Dichas valores son los que se necesitan para que los dos cables ejerzan la misma fuerza
sobre el asiento. Cuanto debe valer aproximadamente la velocidad angular w ?
Ves a la página Péndulo de UNIVERSO FÓRMULAS.
La velocidad angular ω es constante en función de la longitud de la cuerda para pequeñas amplitudes.
ω = &Radic;(g / l)
Para amplitudes mayores, como es tu caso, debes aplicar la corrección del final de la página.
Se tienen cuatro discos unidos mediante una correa de transmisión, como lo
muestra la figura. La medida del radio rojo es 5 cm, del disco azul 20 cm y del
disco verde 10 cm. Si el disco rojo gira con una frecuencia de 120 rpm en
sentido horario, determine:
a) La rapidez tangencial y la angular del disco rojo.
b) La rapidez tangencial y la angular del disco azul.
c) La rapidez tangencial y la angular del disco verde.
d) La dirección y sentido de la velocidad angular del disco verde
e) La frecuencia con la cual gira el disco azul
f) La dirección y sentido de la velocidad angular del disco celeste
figura?
la rueda de una motocicleta da 420 rpm si el radio es de 40cm determinar su periodo la velocidad angular la rapides tangental la aceleracion centripeta ayuda porfa lo necesito para hoy
Gabriel, en esta misma página tienes las fórmulas para hallar directamente lo que necesitas. Y un ejercicio similar que te ayudará.
La velocidad angular en rad/s será:
ω = 420.(2π)/60.
Atrévete con el resto.
Si un disco de 0.8 de diámetro gira con una velocidad tangencial de 45m/s ¿Cuál es su periodo?, ¿Cuál es la frecuencia? Y su velocidad angular
Un motor realiza un trabajo en su operación 2000 revoluciones cada 3 min. Calcular:
Velocidad Angular
Velocidad Tangencial
Aceleración Centrípeta
Con esos datos solamente puedes calcular la velocidad angular.
ω = (2000 * 2 * π) / (3 * 60) rad/s
Tengo una enorme duda. ¿Cuál es la distancia en el
Movimiento circular uniforme?
Por favor iluminenme
Como distancia!
La distancia sería el módulo del vector desplazamiento que une el punto inicial y final. En el MCU esa distancia podría ser cero.
Otra cosa es la distancia recorrida que es el espacio total de la trayectoria.
Piensa en un coche de competición dando vueltas a un circuito. La distancia recorrida serían los kilómetros o millas de la prueba. El desplazamiento podría tener una distancia nula si la linea de salida y de meta fuesen la misma.
buenas consulta. por que en la velocidad tangencial,en las unidades de medidas, no se anotan radianes si no se tachan.gracias
rad/s por cm = cm/ seg rad ?
Las unidades de la velocidad tangencial están anotadas correctamente. Unidades de longitud dividido por unidades de tiempo. En este caso: cm/s.
6d
Tengo una duda, jejeje…
¿cómo calculo la frecuencia? esa realmente no la entendí.
Osea, yo diría que la f:
f:#de vueltas/tiempo empleado
Pero no entiendo muy bien, realmente me confunde
Conviene que tengas claro el sentido de tres magnitudes en cinemática que van ligados entre sí. Los tres los puedes consultar en UNIVERSO FÓRMULAS.
Frecuencia
La frecuencia f es el número de vueltas que recorre la partícula durante una unidad de tiempo. Es la inversa del período.
La unidad de frecuencia es s-1 (se llama ciclo/segundo). También recibe el nombre de hertz o hercio. En mecánica se suele expresar en revoluciones por minuto (r.p.m.).
Velocidad angular
La velocidad angular (ω) es el arco recorrido (θ), expresado en radianes por unidad de tiempo.
Periodo
Se define como período T al tiempo que tarda la partícula en dar una vuelta completa. Es la inversa a la frecuencia.
El período se mide en segundos (s).
Las tres magnitudes vienen ligadas por la fórmula:
T = 1 / f = 2π / ω
Espero habértelo aclarado
Holaaa una pregunta, cuales son las formulas para poder sacar el radio
Todas las que tengas los datos menos el radio r y lo puedas despejar. Por ejemplo:
r = acen / ω²
r = v / ω
Una pregunta, si una rueda lleva una rapidez de 14m/seg y da 140 vueltas en 40, cual seria su periodo?
Como no das el radio, supongo que son 140 revoluciones en 40 segundos. Eso es la velocidad angular ω, que debes pasar a rad / s.
ω = 140 * 2π / 40
El periodo, en segundos, lo hallas con la fórmula de esta misma página.
T = 2π / ω = 4/14 = 2/7 s.
Si tomas una cuerda y la ponemos oscilar con otra más larga cual emple mas tiempo en realizar die oscilaciones?
Esta ecuación del péndulo (péndulo simple) establece que el periodo de oscilación T es proporcional a la raíz cuadrada de la longitud l.
T ≈ 2π√(l / g)
A más longitud, más tiempo empleará en la oscilación.
Me piden que calcule la distancia de una órbita circular, y me dan aceleración centripeta y periodo. Pero no me dan formulas para calcular distancia
¿Cual formula debería usar o que factores debo hallar con la acelaracion y el periodo?
Tienes las fórmulas en esta misma página:
Velocidad angular:
ω = 2π / T
Aceleración centrípeta:
acen = ω² * r
Despeja el radio de la órbita:
r = acen / ω² = acen / (2π / T)²
Podrian compartirme todas las formulas que hay de MCU.
PORFAVOR!
Las tienes en esta página.
Hola, tengo una pregunta, qué relación existe entre velocidad tangencial y velocidad angular? Gracias
Como se indica en esta misma página, la velocidad tangencial es la velocidad angular por el radio.
v = ω * r.
Dicho llanamente, en un disco que gire con una velocidad angular ω, las partes que esten más alejadas del centro de giro (más radio), girarán a mayor velocidad tangencial.
tengo una pregunta porque la aceleración tangencial es 0?
Pincha en aceleración tangencial de esta página.
Verás como en el MCU la velocidad angular ω es constante. No varía. Por lo tanto no hay aceleración tangencial.
¿Como saber si la aceleracion de un objeto en un movimiento circular,es variable o constante?
En un movimento circular, siempre hay una aceleración centrípeta, que será constante mientras la velocidad angular α tambien sea constante.
Otra cosa es la aceleración tangencial, que existirá cuando varie la velocidad (tangencial o angular)
Mira las componentes intrínsecas de la aceleración en UNIVERSO FÓRMULAS
¿Por qué la rapidez lineal en línea recta de un objeto es igual a la rapidez lineal sobre la circunferencia ?
La velocidad, tanto en linea recta, como dices, o lineal como la velocidad tangencial es una magnitud vectorial (tiene un módulo, dirección y sentido). El vector velocidad lineal mantiene su dirección y sentido. El vector de la velocidad tangencial en el movimiento circular cambia constantemente de dirección.
Al módulo de la velocidad se le llama celeridad o rapidez. Es una magnitud escalar. Se mide en unidades de espacio dividido por unidades de tiempo.
Espero haber aclarado la consulta.
Tengo un problema que no puedo resolver y dice
Las poleas estan ligadas por medio de una correa . Si la polea de 16 cm da 8 vueltas cada 4 segundos calcule la frecuencia de la polea de 12 cm
La velocidad angular en la polea 1 será:
ω1 = 8 * 2π / 4 = 12,57 rad/s
Su velocidad tangencial:
v1 = ω*r1 = 12,57 * 0,16 = 2,01 m/s
Las velocidades tangenciales de las dos poleas son iguales. Estan unidas por una correa.
v1 = v2 = 2,01 m/s
La velocidad angular de la segunda polea:
ω2 = v2 / r2 = 2,01 / 0,12 = 16,76 rad/s
La frecuencia de la segunda polea:
ω2 = 2*π*f2
f2 = ω2/2*π = 2,67 ciclos/seg
me puden decir las formulas de movimiento circular
Una pregunta como se calcula el periodo si se tienen por ejemplo 5 vueltas y de tiempo tienes 4.26 s?
Frecuencia (ciclos o vueltas por segundo)
f = 5 vueltas / 4,26 segundos = 1,174 ciclos / segundo
Periodo T es la inversa de la frecuencia f
T = 1 / f = 1 / 1,174 = 0,852 segundos
No entendí nada xD
y el infinito?
no
CON LA FÓRMULA DE LA CAÍDA LIBRE
No se debería colocar la velocidad tangencial como 4 pi rad/sdo.?
Fernando, las unidades de la velocidad tangencial són de espacio/tiempo. Por ej.: cm/s o m/s. Otra cosa son las unidades de la vel. angular, p. ej.: en rad/s. El número π és un número sin unidades que en las fórmulas multiplica o divide como un número más.
Espero que la explicación te sirva.
No valen ni monda eso no lo entendi
Pero si no tienes el radio?…. el profe me dejó un ejercicio de este tipo. :/
el radio es la mitad del diámetro
Está muy buena la explicación… me es muy útil. Gracias… ☺
muy buena didáctica
me sirvió de mucho !!gracias¡¡
Me encanto su trabajo… Y espero q ayuden a muchos mas como lo hicieron conmigo
Busquemos una :*
Muy bien explicado y muy claro.
Cuando encuentras una página con tanta claridad en sus explicaciones uno se siente como en el aula.
MUY BUENA DIDACTICA, EJEMPLO PRACTICO Y CLARO. FELICITACIONES POR APORTAR EN EL CONOCIMIENTO
es buena informacion gracias