
Un polígono irregular es un polígono con los lados y ángulos desiguales.
Elementos del polígono irregular
Se pueden distinguir algunos elementos del polígono irregular:

- Punto interior (P): es cualquier punto que está dentro del perímetro del polígono irregular.
- Lados (Li): son los n segmentos que delimitan al polígono.
- Vértices (Vi): puntos de unión de dos lados. Existen tantos vértices como lados tiene el polígono (n).
- Ángulos interiores (αi): ángulos interiores de la unión de dos lados consecutivos.
Área del polígono irregular
El cálculo del área de un polígono irregular requiere de métodos alternativos de cálculo de áreas. El método más común es dividir el polígono en N triángulos (siendo N el número de lados del polígono) y calcular la área como suma de las áreas de los triángulos.
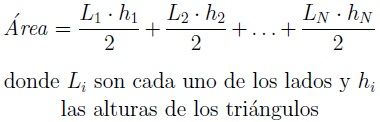
El área del polígono irregular se puede calcular mediante dos procedimientos alternativos: el método de triangulación o el determinante de Gauss:
Triangulación del polígono irregular

Sea P un polígono irregular. Se desea calcular su área (A).
El método de triangulación consiste en dividir el polígono en figuras más fáciles de calcular el área. En este caso se divide en N triángulos y el área del polígono será la suma del área de esos N triángulos.
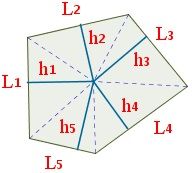
- Se divide el polígono en N triángulos (T1, T2, T3,…, TN) . Estos triángulos cumplen que uno de sus lados es un lado del polígono y que todos confluyen en un mismo punto interior.
- Se miden las alturas (h1, h2,…, hN) de los triángulos. La altura de cada triángulo será el segmento de recta perpendicular al lado del polígono que va desde ese mismo lado hasta el punto interior.
- Se calculan las áreas de los N triángulos. El área del primer triángulo es:

Utilizamos la misma fórmula para calcular el área de los otros N-1 triángulos.
- Sumamos las N áreas y obtenemos el área del polígono irregular:
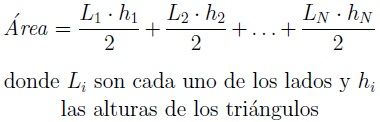



Determinante de Gauss
Un procedimiento muy útil para hallar el área de cualquier polígono irregular es a través del determinante de Gauss.
Supone dibujar la figura sobre un plano cartesiano, fijando las coordenadas de cada uno de los vértices del polígono.

Se elige al azar cualquiera de ellos y se colocan los pares en la siguiente fórmula. Se ha de recorrer el polígono en el sentido contrario al de las agujas del reloj, teniendo en cuenta que el primer par de coordenadas corresponden al vértice elegido y, después de recorrer en sentido antihorario todos los vértices, el último par debe volver a ser el par inicial.
Sean los vértices del polígono: (x1,y1), (x2,y2),…, (xN,yN). La fórmula és la siguiente:

Resolviéndolo por el procedimiento conocido, habremos hallado rápidamente el área del polígono irregular.
Este método es aplicable a cualquier polígono con cualquier número de lados, tanto en el caso de polígonos cóncavos como en los convexos.
Perímetro del polígono irregular
El polígono irregular tiene alguno o todos sus N lados diferentes. Por lo tanto, el perímetro del polígono irregular es la suma de los N lados:


Ejercicios resueltos
Ejercicio del perímetro de un polígono regular

Sea un polígono irregular con seis lados (N=6) no todos iguales, siendo sus longitudes: L1=2,1 cm, L2=2,7 cm, L3=3,4 cm, L4=2,9 cm, L5=2,4 cm y L6=3,0 cm.
El perímetro del polígono irregular será la suma de todos sus lados:
Como resultado obtenemos que su perímetro es de 16,5 cm.

entonces un poligono irregular no tiene centro?
No como tal.
En todo caso tendría un centroide (Ver la página en UNIVERSO FÓRMULAS).
Buenas tardes, tengo las coordenadas de todas los vértices del polígono irregular, leí la información de como calcular el área con Gauss, lo que me sirvió perfectamente, la pregunta que me gustaría me ayuden a resolver es:
si tengo el valor (x,y) (coordenada) de un punto cualquiera, es posible determinar si pertenece al interior del polígono o si no pertenece al interior del polígono? , esto tomando en cuenta que el polígono evaluado es un polígono cóncavo.
La determinación del interior de un polígono es un problema topológico que rebasa los propósitos de esta web. Lo siento.
Como saco el punto interior del poligono irregular? antes de dividirlo en triangulos
Es una construcción geométrica a criterio de quien
la practica. El trabajo con los triángulos viene después.
Lo ideal sería conocer las coordenadas de los vértices y resolver por el determinante de Gauss.
¿cuales son las medidas de los ángulos interiores de un polígono con los ángulos exteriores si sus medidas son de 50° y 40°?
Datos insuficientes
Como sería la fórmula para encontrar la distancia de dos puntos, de un polígono irregular, en un plano cartesiano, solo se que es:
D: raíz cuadrada (X²-X¹) + (Y²-Y¹)
Pero si tiene más lados que resolver, es lo mismo, o cambiaría ?
La fórmula que expones es la de la distancia entre dos puntos en el plano cartesiano. Mira la página Recta en UNIVERSO FÓRMULAS, en particular, en el apartado Distancia entre dos puntos de una recta . Basada en el teorema de Pitágoras.
La fórmula genérica es la misma para la distancia de cualquier lado de un polígono irregular, siempre que conozcas las coordenadas de sus vértices.
como se encuentra el angulo interno de un polígono irregular?, cual es su formula
No tiene porqué haber un ángulo interno en un polígono irregular. Y no existe tal fórmula.
La regla para saber las medida de los ángulos internos de un polígono regular ¿cuál es?
Visita la página : ángulos interiores de un polígono de UNIVERSO FÓRMULAS. Allí encontrarás la fórmula de los regulares.
Si tengo una geometría no homogénea, donde existen infinidad de lados, cómo podría saber el centro de esa forma? Conozyo sólamente la distancia máxima, la cual no necesariamente pasa por el centro de la figura. Y conozco el volumen también. Alguien podría apoyarme para saber cómo calcular el centro de esa figura?, por favor. Saludos.
Teniendo los lados pero no las alturas cómo puedo calcular el Area ???
Sólamente con los lados, si el polígono es irregular, no se puede calcular el área.
profesor eso esta muy largo atentamente rachel
me vale mantequilla este post
Para averiguar el perímetro, de un poligono irregular pero no me dan las medidas de todos sus lados , como lo resuelvo??
GRACIAS!!
Lo siento Carolina. Como dices, teniendo siquiera n-1 lados y ningún dato más, no tienes solución.
eres una pura
apesta no me gsto
Buenas tardes!
Te hago una consulta como seria si quisiera obtener la propagación de error de este polígono irregular.
Muchas gracias de antemano
Lo siento, Pedro, pero el cálculo de la propagación de error rebasa en estos momentos los objetivos de UNIVERSO FÓRMULAS.
si se las medidas, auque sean diferentes puedo aplicar P*a/2
osea sumo susmedidas desiguales
No puedes aplicar ls fórmula. Un polígono irregular no tiene apotema.
No serìa viable cubìcar el polìgono? Luego sumar sus lados y dividirlo por cuatro. Y aplicamos la formula lado al cuadrado.
Si tu propuesta es construir un cubo cuyo perímetro sea el del polígono de partida, la respuesta es que el área de ese cubo y el del polígono irregular con perímetro igual no tienen la misma área (salvo una improbable casualidad).
Cuál es la magnitud del polígono irregular
un hexágono irregular, ¿tiene un ángulo central que mide 60°? o solo mide 60° con el regular?
muy bueno me sirvio de mucho….excelente pagina…gracias
Entonces, en conclusion, el poligono irregular tiene angulo central?
gracias me ayudo mucho
Como calcular la longitud de uno de los lados ? Teniendo a los otros 3 siendo todos lados diferentes?
Como sacar el área de un polígono
Puedes encontrar las fórmulas del área de un polígono aquí.