Área de un pentágono

Un pentágono es un polígono de cinco lados. El cálculo del área de un pentágono es diferente dependiendo de si el pentágono es regular o irregular.

Área del pentágono regular

El área del pentágono regular es un medio del perímetro por la apotema (ap), utilizando la fórmula del área del poligono regular.

Al ser su perímetro cinco veces la longitud (L) de uno de sus lados, el área será:

Como la apotema del pentágono regular se calcula con esta fórmula (a partir de la apotema de un polígono regular):

Donde α es el ángulo interior del pentágono regular. Así, la fórmula del área del pentágono regular también se puede expresar:

Área de un pentágono irregular

El cálculo del área de un pentágono irregular requiere de métodos alternativos de cálculo de áreas. El más común es dividir el pentágono en cinco triángulos y calcular el área sumando las cinco áreas de los triángulos.

Podemos calcular el área del pentágono irregular mediante dos procedimientos alternativos: el método de triangulación o el determinante de Gauss.

Triangulación del pentágono irregular

Sea P un pentágono irregular. Se desea calcular su área (A).

El método de triangulación consiste en dividir el pentágono en figuras más fáciles de calcular el área. En este caso se divide en cinco triángulos y el área del pentágono será la suma del área de esos cinco triángulos.

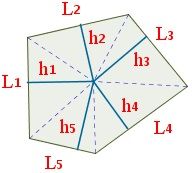
1. Se divide el pentágono en cinco triángulos (T₁, T₂, T₃, T₄ y T₅) . Estos triángulos cumplen que uno de sus lados es un lado del pentágono y que todos confluyen en un mismo punto interior del pentágono.



2. Se miden las alturas (h₁, h₂,…, h₅) de los triángulos. La altura de cada triángulo será el segmento de recta perpendicular al lado del pentágono que va desde ese mismo lado hasta el punto interior.



3. Se calculan las áreas de los cinco triángulos. El área del primer triángulo es:
   

   Utilizamos la misma fórmula para calcular el área de los otros cuatro triángulos.

4. Sumamos las cinco áreas y obtenemos el área del pentágono irregular:
   

Determinante de Gauss

Un procedimiento muy útil para hallar el área de cualquier polígono irregular es a través del determinante de Gauss.

Supone dibujar la figura sobre un plano cartesiano, fijando las coordenadas de cada uno de los vértices del polígono.

Se elige al azar cualquiera de ellos y se colocan los pares en la siguiente fórmula. Se ha de recorrer el polígono en el sentido contrario al de las agujas del reloj, teniendo en cuenta que el primer par de coordenadas corresponden al vértice elegido y, después de recorrer en sentido antihorario todos los vértices, el último par debe volver a ser el par inicial.

Sean los vértices del pentágono: (x₁,y₁), (x₂,y₂),…, (x₅,y₅). La fórmula es la siguiente:

Resolviéndolo por el procedimiento conocido, habremos hallado rápidamente el área del pentágono irregular.

Este método es aplicable a cualquier polígono con cualquier número de lados, tanto en el caso de polígonos cóncavos como en los convexos.

Ejercicio del área del pentágono regular

Sea un pentágono regular con los cinco lados (N=5) de la misma longitud L=3,6 cm.

La apotema (distancia del centro del pentágono al punto medio de un lado) se puede calcular mediante el ángulo central (resolución del polígono regular trigonométricamente).

Sea el ángulo central:

Mediante las razones trigonométricas y el ángulo central se calcula la apotema:

Y la apotema es ap=2,48 cm.

Se aplica la fórmula del área del pentágono regular:

Y se obtiene que el área es 22,30 cm².