El muestreo estratificado es un tipo de muestreo probabilístico. Los individuos de toda la población se dividen en grupos o estratos. Cada elemento pertenece a un único estrato. La variable elegida para formar los estratos no debe permitir que un individuo o elemento de la población pertenezca a más de uno de ellos.
La variable elegida deberá ser significativa para el motivo u objetivo del estudio o investigación.
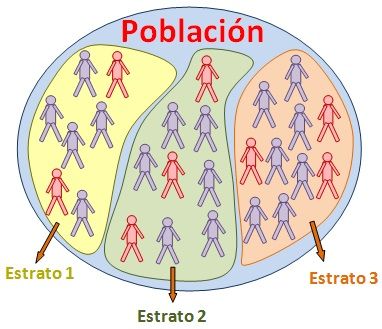
La muestra se elige escogiendo en cada estrato un número representativo de individuos. El tamaño de la muestra se fijará mediante uno de los tipos de muestreo disponible. La elección de los elementos en cada estrato se realiza mediante algún método de muestreo aleatorio simple o muestreo sistemático.
Suponemos que hay k estratos de tamaños N1, N2,…, Nk, de forma que:
En cada estrato se toman n1, n2,…, nk elementos para la muestra, de manera que se toman en total n individuos, es decir:
Número de sujetos por estrato
Se tomará una muestra que sea representativa del conjunto de la población. El número de individuos que se eligen de cada estrato se puede decidir mediante diversos criterios:
- Elección simple (o uniforme): se toman de la muestra el mismo número de sujetos para cada uno de los k estratos. De cada estrato se seleccionarían n/k individuos. Este criterio no es recomendable cuando los estratos tienen un número de individuos significativamente diferente.
Por ejemplo, en una muestra de 900 individuos dividida en tres estratos, cada uno de ellos tendría 900/3 = 300 elementos.
- Elección proporcional al tamaño del estrato: el tamaño de la muestra en cada grupo es proporcional a los elementos de dicho grupo. En cada estrato se tomarán ni elementos, calculados mediante la fórmula:

Por ejemplo, suponemos que se está haciendo un estudio sobre la toma de pastillas para dormir en una ciudad de 100.000 habitantes. La variable edad se considera adecuada para obtener resultados en esta investigación. Se incluyen solamente los mayores de 40 años en el estudio. Se distribuyen en tres grupos o estratos, resultando una agrupación, según el censo:

Por el procedimiento de muestreo elegido obtenemos una muestra de 750 sujetos. Para asignar el número de componentes a los tres estratos de edad, aplicaremos la fórmula anterior:

Donde n / N es una constante llamada razón de muestreo, que en este caso es de 0,015.
Resulta una distribución muestral por estratos tal que así:

- Elección proporcional a la variabilidad del estrato: si se conoce la variabilidad de la característica o variable que estamos tomando en cuenta en cada estrato, se toman los sujetos proporcionalmente a la variabilidad en cada grupo. En los grupos donde la varianza sea mayor, se toman, por tanto, más sujetos.

Cuando utilizarlo
- Se utiliza el método de muestreo estratificado cuando los elementos se dividen en estratos según la variable o variables que se está estudiando.
Por ejemplo, supongamos que se hace una encuesta para las elecciones en EEUU y se sabe que el candidato demócrata tiene mayor influencia en las mujeres que el candidato republicano. La muestra de la encuesta debería estratificarse en hombres y mujeres, puesto que sabemos que la variable género influye en la votación.
- En las encuestas conocemos datos sobre variables relacionadas con el estudio, como la edad, sexo, nivel socioeconómico. Conviene que la muestra tenga una composición proporcional a los individuos de cada estrato.
- Se utiliza el muestreo estratificado cuando los grupos o estratos son muy homogéneos internamente y diferentes entre ellos. Si los grupos, internamente son muy heterogéneos y no existen muchas diferencias entre ellos, es recomendable utilizar el muestreo por conglomerados.
- El muestreo estratificado tiene una precisión mayor que el muestreo aleatorio simple. Es debido a la mayor homogeneidad dentro de cada grupo o estrato respecto a la totalidad de la población. Requiere, debido a su precisión, un tamaño de la muestra menor. Por el contrario, el muestreo estratificado es más costoso y requiere más tiempo, tanto para el conocimiento de los estratos como para la definición de las variables.
Diferencia con el muestreo por cuotas
El muestreo estratificado se diferencia del muestreo por cuotas en que una vez se decide el número de sujetos que se van a elegir de cada estrato, en el método de muestreo estratificado se eligen los individuos aleatoriamente y en el muestreo por cuotas no.
El muestreo estratificado es más costoso, pero más indicado cuando la población es muy heterogénea y hay estratos con diferencias significativas respecto a otros estratos.

Pingback: 📈 Muestreo estratificado + ejemplo explicado paso a paso
Buenísimo, muchas gracias por el aporte
Creo que hay muchas imprecisiones tanto en el documento como en algunos comentarios. Se supone que la población ha sido dividida en L estratos que son más homogéneos que la población misma pero que deben estar bien determinados. Es decir, debe haber un marco muestral claramente establecido y los tamaños Ni de tales estratos deben estar plenamente definidos. N, el tamaño de la población, es la suma de los Ni. Una manera frecuente para calcular el tamaño n de la muestra es usar una muestra preliminar pequeña que se selecciona tomando bajo muestreo aleatorio simple, pequeñas muestra de cada estrato. Existen fórmulas que permiten calcular el tamaño n y realizar una afijación óptima, que siempre es la más recomendable. Esta afijación se hace proporcional al tamaño de los estratos y a las varianzas en los mismos e inversamente proporcional a los costos de muestreo en cada estrato. Las fórmulas pueden consultarse , por ejemplo en W.Cochran, «Sampling Tecniques». exelente libro que, a pesar de los años, sigue marcando tendencia en el estudio del muestreo. Existe versión española del mismo
Buenas tardes.
Para un caso de estudio estoy usando el muestreo estratificado, pero resulta que mis subconjuntos tienen otras variables, es decir, más estratos que debo considerar y creo que la fórmula que exponen aquí ya no me serviría, entonces cómo sería la fórmula que debo aplicar. Muchas gracias.
Puedes utilizar varias variables de estratificación, siempre que sean coherentes con el objeto de la investigación. El número de variables debe ser limitado, para que los efectos de una no condicione o altere los efectos de otra. No debieran ser más de cinco, como extremo, seis. A su vez, dentro de cada variable no deberían haver más de cinco o seis estratos.
Una vez hecha la división, aparecerán un número de estratos en los que no debe de repetirse ningún elemento.
Y ya tienes hecha la división de tu muestreo estratificado.
Puede ser un muestreo imaginario?
de donde sale el 750
Es un tamaño muestral, supuesto para explicar el procedimiento de asignar los estratos.
Consulta la página tamaño de la muestra en UNIVERSO FÓRMULAS para ver métodos para hallar el tamaño de la muestra para estimar una proporción o estimar una media.
No entiendo la fórmula de elección proporcional a la variabilidad del estrato. A qué de refiere Ni?
Ni es el número de elementos del estrato i.
De los tres procedimientos para hallar el número de elementos de cada estrato, el proporcional a la variabilidad del estrato es cuando la conoces y difiere en los diferentes estratos, por lo que debe tenerse en cuenta.
Ola tengo una duda yo ya tengo mi población y quiero evaluara a niños pero sus diferentes grados en la escuela como lo podría hacer, como calcularía la muestra por conglomerados?
Las fórmulas para calcular los n(i) están mal, pues para calcularlas se requiere del valor de n (el número de elementos de la muestra) que a su vez es la suma de las n(i)!!!
Cocuerdo con esta apreciacion, como calcular n(i) si no conozco n tampoco?
algo con lo que quedaría aun mejor seria aplicar ejemplos a las definiciones en mi caso no se si «Elección proporcional a la variabilidad del estrato» es lo que necesito para seleccionar la muestra a nivel sexual de un estrato, es decir tengo una población entre edades de 20 y 25 y ya tengo la muestra gracias a los ejercicios, pero, ahora necesito dividir la muestra de este mismo estrato a nivel sexual, es decir, seleccionar cuantos hombres y cuantas mujeres serian seleccionadas en esa muestra.
tienes la bibliografia de esto
Parece que hay un error de tipeo, en la sección «Cuándo Utilizarlo» mencionan que: «Si los estratos son agrupaciones naturales y la característica que estudiamos puede ser homogénea en cada uno de los grupos, nos podemos plantear utilizar el método de muestreo por conglomerados. El método por estratificación funciona mejor cuando más diferentes sean los estratos. El muestreo por conglomerados es mejor cuando los grupos son más HETEROGENOS»,
Prmero dicen que cuando las características son homogéneas usar Conglomerados, pero al fnal dicen heterog´éneas.
De todas formas muchas gracias, me sirvió bastante las fórmulas para calcular mi muestra por estratos. Gracias.
Tienes razón Oscar.
A parte de que hemos incurrido en una contradicción, estaba mal explicado y confundía.
Lo hemos cambiado y lo hemos explicado mejor, esperamos que así se entienda mejor.
Muchas gracias por avisarnos y disculpad las molestias.
Un saludo.
eso te puede ayudar
GENIAL!! :3 Este sitio esta Bien Chido 🙂