La energía es la capacidad de un cuerpo o de un sistema de cuerpos para generar un trabajo. Energía y trabajo son magnitudes equivalentes, por lo que se expresarán con las mismas unidades.
Energía cinética
La energía cinética es una magnitud escalar y es la capacidad de un cuerpo en movimiento para generar un trabajo. O, en otras palabras, un cuerpo en movimiento posee energía cinética. Pensemos en un taco de billar en movimiento, que es capaz de generar el trabajo de impulsar una bola al impactar con ella.
La ecuación, en mecánica, para calcularla es:

¿Cómo se obtiene?
A partir de la ecuación fundamental de la dinámica, o segunda ley de Newton:

Como el trabajo W realizado por la fuerza F es igual a la energía cinética Ec que adquiere el cuerpo:
Sustituyendo en las ecuaciones anteriores, tendremos:

A partir de esto se deriva el siguiente teorema.
Teorema de la energía cinética
El trabajo que realiza una fuerza sobre una masa inicialmente en reposo es igual a la energía cinética que adquiere ese cuerpo.
Otra formulación del mismo teorema es:
El trabajo realizado por la fuerza sobre un cuerpo de masa m es igual a la variación de su energía cinética.

(v1 es la velocidad inicial y v2, la velocidad final. La fuerza no tiene porqué ser constante).
Ejercicio
Un guepardo de 50 kg corre tres una gacela a 100 km/h. ¿Cuál es su energía cinética?

Solución:
Aplicamos la fórmula que hemos expuesto anteriormente, transformando las unidades de velocidad.

El guepardo ha adquirido una energía cinética de 19.290,12 J.
Energía potencial
En mecánica, la energía potencial es la capacidad que tiene un cuerpo para realizar un trabajo en función de su posición. Podemos distinguir dos clases de energía potencial: la energía potencial gravitatoria y la energía potencial elástica.
Energía potencial gravitacional
En el campo de gravedad terrestre, llamamos energía potencial gravitatoria de un cuerpo en un punto, a la que posee respecto al punto de referencia que es el nivel de la superficie de la Tierra. Si partimos de ese nivel y elevamos una masa m hasta una altura h, esa masa adquiere una energía potencial. Su expresión es:
Donde g es la aceleración de la gravedad ( a nivel del mar, g = 9.81 m/s2).
¿Cómo se obtiene?
De las ecuaciones del MRUV tenemos las fórmulas siguientes:

Se sustituye aquí la aceleración a por g y el espacio o posición x por h).
Despejando t en la primera y sustituyéndola en la segunda, tenemos:
Como la energía cinética que adquiriria al llegar al suelo el cuerpo si se le soltase desde la altura h sería:

Sustituyendo la expresión de la velocidad v que tendría en el momento del impacto, resulta:

Sólo se puede medir variaciones de energia potencial gravitatoria, ya que se toma su variación desde puntos de referencia. Seguiría disminuyendo si, desde el nivel del mar dejásemos caer el cuerpo en un pozo.
Ejercicio
Entre un ciclista y su bicicleta pesan 75 kg. Hallar la energía cinética que posee el conjunto ciclista-máquina cuando el ciclista pedalea a una velocidad de 25 km/h.
Calcular el aumento de su energía potencial cuando, desde un recorrido en llano, sube una rampa de 200 m de desnivel.
Solución:

La energía cinética será:

El aumento de energía potencial gravitacional:
Energía potencial elástica
La energía potencia elástica es la capacidad que tiene un cuerpo elástico (resorte, muelle, un arco, etc.) para realizar un trabajo según de la posición en que se encuentre respecto a su posición de equilibrio. O, dicho de forma inversa, la energía potencial elástica que tiene un muelle, un resorte, etc. es igual al trabajo que ha realizado una fuerza externa a él para causarle esa deformación. Esta energía potencial es proporcional al cuadrado de la deformación producida.
La variación de la energía potencial elástica de un sistema (por ejemplo un muelle-peso) es el valor negativo del trabajo realizado por una fuerza conservativa (fuerza recuperadora del muelle).
Su expresión es:

Donde k es la constante elástica o constante recuperadora del muelle y x el desplazamiento.
La constante k es propia de cada muelle o resorte. Depende de la longitud del muelle, su composición, temperatura, geometría, etc. Usualmente, sus unidades son N/m.
Ley de Hooke
Cuando, debido a una fuerza externa, un resorte sufre una deformación respecto a su posición de equilibrio, la fuerza recuperadora que ejerce este muelle o resorte es directamente proporcional al cambio de longitud. La fuerza recuperadora es una fuerza conservativa.
El signo negativo es debido a que el sentido de la fuerza recuperadora es de sentido contrario a la deformación (o elongación, o desplazamiento, o alargamiento).
k es la constante elástica. Es propia de cada muelle y sus unidades suelen ser N/m.
- Muelle en posición de equilibrio:
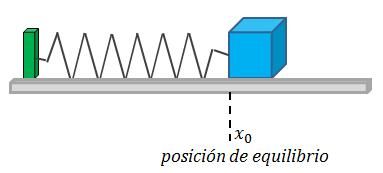
- Muelle después de que una fuerza externa haya producido una deformación:

Esta ley es válida siempre que no se rebase el límite elástico del muelle o resorte.
La deformación elástica es cuando, al retirar la fuerza exterior, el muelle, o material en general, recupera la forma inicial. La deformación elástico-plástica es un intervalo de esfuerzo intermedio que no produce una deformación irreversible, aunque no se vuelve a la forma inicial.
La deformación plástica se produce cuando se aplica una fuerza tal que cuando ésta se retira, la deformación queda irreversible. Esto se puede ver en el gráfico:

La ley de Hooke se cumple en la zona elástica.
Se utilizan los parámetros unitarios esfuerzo o tensión, σ y deformación o alargamiento unitario ε. Sus expresiones son:
- La fórmula del esfuerzo, que es la fuerza por unidad de superficie de la sección transversal del resorte (no producirá el mismo efecto una fuerza F sobre un alambre de 2 mm2 de diámetro que sobre otro de 3 mm2 de diámetro.

- La fórmula de la deformación, que es la relación entre la variación de longitud y la longitud total. (No es lo mismo un alargamiento de 2 cm al estirar de un alambre de 1 m de longitud que el mismo alargamiento, tirando con la misma fuerza, de un alambre de 4 m.

- La fórmula del módulo de Young:

Ejercicio
Un muelle en reposo mide 20 cm.

Al colgarle un cuerpo de 1 kg su longitud es ahora de 30 cm.

- Calcular la constante recuperadora, k.
- ¿Cuál será la longitud del muelle si después le colgamos un cuerpo de 3 kg?

Solución:
Primero se calcula k, igualando la fuerza peso con la fuerza recuperadora del muelle, pues el conjunto queda inmóvil tres el primer alargamiento:

Conociendo k, hallaremos el segundo alargamiento:

Y la longitud total del muelle será:
Una longitud del muelle con la segunda carga de 50 cm.
