La energía potencia elástica es la capacidad que tiene un cuerpo elástico (resorte, muelle, un arco, etc.) para realizar un trabajo según de la posición en que se encuentre respecto a su posición de equilibrio. O, dicho de forma inversa, la energía potencial elástica que tiene un muelle, un resorte, etc. es igual al trabajo que ha realizado una fuerza externa a él para causarle esa deformación. Esta energía potencial es proporcional al cuadrado de la deformación producida.
La variación de la energía potencial elástica de un sistema (por ejemplo un muelle-peso) es el valor negativo del trabajo realizado por una fuerza conservativa (fuerza recuperadora del muelle).
Su expresión es:

Donde k es la constante elástica o constante recuperadora del muelle y x el desplazamiento.
La constante k es propia de cada muelle o resorte. Depende de la longitud del muelle, su composición, temperatura, geometría, etc. Usualmente, sus unidades son N/m.
Ley de Hooke
Cuando, debido a una fuerza externa, un resorte sufre una deformación respecto a su posición de equilibrio, la fuerza recuperadora que ejerce este muelle o resorte es directamente proporcional al cambio de longitud. La fuerza recuperadora es una fuerza conservativa.
El signo negativo es debido a que el sentido de la fuerza recuperadora es de sentido contrario a la deformación (o elongación, o desplazamiento, o alargamiento).
k es la constante elástica. Es propia de cada muelle y sus unidades suelen ser N/m.
- Muelle en posición de equilibrio:
- Muelle después de que una fuerza externa haya producido una deformación:

Esta ley es válida siempre que no se rebase el límite elástico del muelle o resorte.
La deformación elástica es cuando, al retirar la fuerza exterior, el muelle, o material en general, recupera la forma inicial. La deformación elástico-plástica es un intervalo de esfuerzo intermedio que no produce una deformación irreversible, aunque no se vuelve a la forma inicial.
La deformación plástica se produce cuando se aplica una fuerza tal que cuando ésta se retira, la deformación queda irreversible. Esto se puede ver en el gráfico:

La ley de Hooke se cumple en la zona elástica.
Se utilizan los parámetros unitarios esfuerzo o tensión, σ y deformación o alargamiento unitario ε. Sus expresiones son:
- La fórmula del esfuerzo, que es la fuerza por unidad de superficie de la sección transversal del resorte (no producirá el mismo efecto una fuerza F sobre un alambre de 2 mm2 de diámetro que sobre otro de 3 mm2 de diámetro.

- La fórmula de la deformación, que es la relación entre la variación de longitud y la longitud total. (No es lo mismo un alargamiento de 2 cm al estirar de un alambre de 1 m de longitud que el mismo alargamiento, tirando con la misma fuerza, de un alambre de 4 m.

- La fórmula del módulo de Young:

Ejercicio 1
Un muelle en reposo mide 20 cm.

Al colgarle un cuerpo de 1 kg su longitud es ahora de 30 cm.

- Calcular la constante recuperadora, k.
- ¿Cuál será la longitud del muelle si después le colgamos un cuerpo de 3 kg?

Solución:
Primero se calcula k, igualando la fuerza peso con la fuerza recuperadora del muelle, pues el conjunto queda inmóvil tres el primer alargamiento:

Conociendo k, hallaremos el segundo alargamiento:

Y la longitud total del muelle será:
Una longitud del muelle con la segunda carga de 50 cm.
Ejercicio 2
Un muelle está fijo sobre una superficie lisa. Una bola de 100 gr se comprime contra el muelle, haciéndolo retroceder 6 cm. La constante recuperadora del muelle es k es 200 N/m. Si ahora soltamos, el muelle salta, empuja a la bola y regresa a su posición inicial. ¿A qué velocidad abandonará la bola el contacto con el muelle?
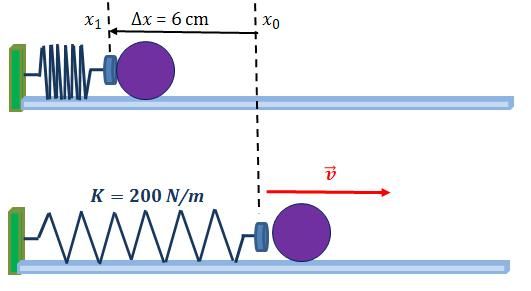
Solución:
En primer lugar se calcula la energía potencial elástica que se ha almacenado en el muelle al ser comprimido:

Al liberar el muelle, esa energía potencial elástica del sistema muelle-bola es trasmitida a la bola que queda libre, transformándose la energía en energía cinética que adquiere la bola:

Finalmente, calcular la velocidad de salida de la bola.

La bola sale disparada del muelle a 2,68 m/s.
Ejercicio 3
Calcular la energía potencial total almacenada en el primer ejercicio, sabiendo que el centro de gravedad de la masa de 3 kg ha quedado a 1,5 m sobre el suelo (despreciar el peso del muelle).
(Recordemos que cuelga de un muelle con una constante recuperadora k de 98,1 N/m y que ha producido en el muelle un alargamiento de 30 cm sobre su posición de reposo).

Solución:
La energía potencial total será la suma de la energía potencial elástica del muelle y la energía potencial gravitatoria de la masa.

La masa colgada de 3 kg y el muelle alargado han almacenado una energía potencial total de 48,56 J.

Exelente la explicación, muy sencilla
Tengo una inquietud. Si un resorte se encuentra sujetado horizontalmente en una superficie lisa y es jalado por un cuerpo de 2 Kg, a través de una cuerda y una polea sin rozamiento, que desciende por un plano liso e inclinado 37°. ¿Cuál es la elongación que sufre el resorte? (determinar por factores energéticos y demostrar por análisis de un sistema de fuerzas estacionario)
Una pista:
La fuerza que la masa de 2 kg tensa la cuerda al deslizarse por el plano inclinado es de: 2g sen 37°
La elongación del resorte (ley de Hooke):
Δx = -2g sen 37° / k
k es la constante elástica del resorte y el signo – es porque el sentido de la deformación es contraria a la fuerza conservadora del muelle.
muy bueno
Muy buena informacion, esta genial!!