Existen los siguientes tipos de funciones:
- Función polinómica
- Función radical
- Función inversa
- Funciones trascendentes
- Funciones definidas a trozos
- Función derivada
- Funciones inyectivas, sobreyectivas y biyectivas
- Funciones explícitas e implícitas
- Función valor absoluto
Función polinómica
Una función polinómica f es una función cuya expresión es un polinomio tal como:

El dominio de las funciones polinómicas son todos los números reales.
Las funciones polinómicas son continuas en todo su dominio.
Se llama grado de una función polinómica al mayor exponente de sus términos. Por ejemplo, el polinomio de la función del gráfico de arriba es de grado 3.
Los diferentes ai (a0, a1, …an), son números reales llamados coeficientes de un polinomio.
Función constante
Una función f es constante si la variable dependiente y toma el mismo valor a para cualquier elemento del dominio (variable independiente x).

En términos matemáticos, la función f es constante si para cualquier par de puntos x1 y x2 del dominio tales que x1<x2, se cumple que f(x1) = f(x2).

La gráfica de una función constante es una recta paralela al eje de abscisas X.
Función polinómica de primer grado
Las funciones polinómicas de primer grado o de grado 1 son aquellas que tienen un polinomio de grado 1 como expresión. Están compuestas por un escalar que multiplica a la variable independiente más una constante. Su mayor exponente es x elevado a 1.


Su representación gráfica es una recta de pendiente m.
La m es la pendiente y la n la ordenada, o punto en donde corta la recta f al eje de ordenadas. Según los valores de m y n existen tres tipos:
Función afín
Una función afín es una función polinómica de primer grado que no pasa por el origen de coordenadas, o sea, por el punto (0,0).
Las funciones afines son rectas definidas por la siguiente fórmula:
Los escalares m y n son diferentes de 0.

Función lineal
Una función lineal es una función polinómica de grado 1 que pasa por el origen de coordenadas, es decir, por el punto (0,0). Son funciones rectas de la forma:


También se llaman funciones de proporcionalidad directa. La constante m es la razón de proporcionalidad.
El término independiente n de la función afín es cero.
Función identidad
Una función identidad es una función tal que la imagen de cualquier elemento es éste mismo:
Estas funciones también suele denotarse por id.

La función identidad es una función lineal de pendiente m = 1 que pasa por el origen de coordenadas, es decir, por el punto (0,0). Divide el primer y el tercer cuadrante en partes iguales, o sea, es su bisectriz.
La función identidad es importante en la función inversa.
Función cuadrática
Las funciones cuadráticas (o funciones de segundo grado) son funciones polinómicas de grado 2, es decir, el mayor exponente del polinomio es x elevado a 2 (x2):

Su representación gráfica es una parábola vertical.

Una función cuadrática puede tener dos raíces reales, una o ninguna. Las raíces de una función son los elementos del dominio que la hacen nula. Es decir, son los puntos donde la gráfica de la función corta al eje X.
Función cúbica
Las funciones cúbicas (o funciones de tercer grado) son funciones polinómicas de grado 3, es decir, las que el mayor exponente del polinomio es x elevado a 3 (x3):

La representación gráfica de la función cúbica es:

Una función cúbica puede tener tres raíces reales dos o una. Las raíces de una función son los elementos del dominio que la hacen nula. Es decir, son los puntos donde la gráfica de la función corta al eje X.
Función racional
Las funciones racionales f(x) son el cociente irreducible de dos polinomios (para ello, no deben tener las mismas raíces). La palabra racional hace referencia a que esta función es una razón.

P(x) es el polinomio del numerador y Q(x) el del denominador (La variable x debe de estar en el denominador).
El dominio de una función racional son todos los números reales excepto los valores de la variable x que anulan el denominador (Q(x)) = 0), es decir, excepto las raíces del polinomio correspondiente al denominador.
La gráfica de estas funciones, si el polinomio del denominador Q(x) es de grado 1, es una hipérbola:

(En todas las funciones racionales en las que el grado del polinomio del numerador P(x) sea el mismo que grado del del denominador Q(x), existe una asíntota horizontal y = a / k, siendo aquí a y k los coeficientes de los términos de mayor grado de P(x) y de Q(x)) respectivamente.

Función de proporcionalidad inversa
Una función de proporcionalidad inversa es la que, cuando la variable dependiente y es igual a una constante dividida por la variable independiente x . Su expresión es:

k es el coeficiente de proporcionalidad inversa.
Su dominio y su codominio son los números reales, excepto en las asíntotas (x = 0 e (y = 0) en donde hay un punto de ruptura y el denominador es nulo.
La derivada de la función de proporcionalidad inversa es:

Si k > 0, la función es decreciente y está en el primer y tercer cuadrante.

Si k < 0, la función es creciente y está en el segundo y cuarto cuadrante.

La gráfica es una hipérbola equilátera con una asíntota vertical y otra horizontal en los dos ejes de coordenadas.
Función radical
Una función radical o función raíz es la que la variable dependiente y se obtiene de una raíz que alberga en el radicando a la variable independiente x.
Son llamadas también funciones irracionales.
Cuando el índice de la raíz n es par, el dominio de la función son los valores de x que hacen al radicando cero o mayor que cero.

Cuando el índice es impar, el dominio son los números reales.
Un ejemplo de gráfica de función radical con índice n impar:

Función inversa
Sea f una función que asigna a los elementos de un primer conjunto (conjunto inicial X) un elemento de un segundo conjunto (conjunto final Y). La función inversa (o función recíproca) de f (denotada por f-1) es aquella que hace el camino inverso, asignando a los elementos de Y elementos de X.

Formalmente, diremos que f-1 es la inversa de f si:
También podemos definir una función inversa a partir de la composición de funciones. f-1 es la inversa de f y f-1 si la composición de f da la función identidad.
Para que una función f tenga inversa necesariamente debe ser inyectiva.
Funciones trascendentes
Una función trascendente es la que la variable independiente x se encuentra en el exponente, el índice de una raíz, en un logaritmo o en una función trigonométrica.
Para una función trascendente no basta con operaciones algebraicas, sino que se requieren cálculos como derivadas, integrales, trigonometría, etc.
Son funciones trascendentes las exponenciales, las potenciales exponenciales, logarítmicas o las trigonométricas.
Función exponencial
Una función exponencial es aquella en que la variable independiente x aparece en el exponente y tiene de base una constante a. Su expresión es:
Siendo a un real positivo, a > 0, y diferente de 1, a ≠ 1.

La función potencial exponencial es aquella en la que, tanto la base como el exponente son funciones. Dicho de otra manera, la variable independiente x se encuentra en la base y en el exponente. Su forma genérica es:
Estas son dos gráficas de la función potencial exponencial. Una, más simple y otro ejemplo cualquiera:

Función logarítmica
Una función logarítmica está formada por un logaritmo de base a, y es, en su forma simple, de la forma:
siendo a un real positivo, a > 0, y diferente de 1, a ≠ 1.

La función logarítmica es la inversa de la función exponencial.
Funciones trigonométricas
las funciones trigonometricas f son aquellas que están asociadas a una razón trigonométrica.

Las razones trigonométricas de un ángulo α son las obtenidas entre los tres lados de un triángulo rectángulo. Es decir, las comparaciones por su cociente de sus tres lados a, b y c.
Existen seis funciones trigonométricas:
Seno

El seno de un ángulo α se define como la razón entre el cateto opuesto (a) y la hipotenusa (c).

Su abreviatura son sen o sin (del latín sinus).
La gráfica de la función seno es:
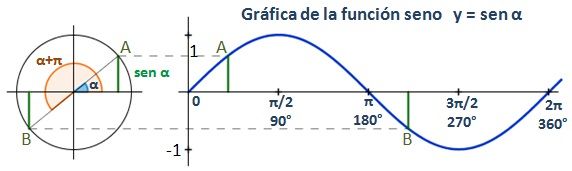
La función del seno es periódica de período 360º (2π radianes), por lo que esta sección de la gráfica se repetirá en los diferentes períodos.
- Dominio:

- Codominio:

- Derivada de la función seno:

- Integral de la función seno:

Coseno

El coseno de un ángulo α se define como la razón entre el cateto contiguo o cateto adyacente (b) y la hipotenusa (c).

Su abreviatura es cos (del latín cosinus).
La gráfica de la función coseno es:

La función del coseno es periódica de período 360º (2π radianes).
- Dominio:

- Codominio:

- Derivada de la función coseno:

- Integral de la función coseno:

Tangente

La tangente de un ángulo α es la razón entre el cateto opuesto (a) y el cateto contiguo o cateto adyacente (b).

Su abreviatura son tan o tg.
La gráfica de la función tangente es:

La función de la tangente es periódica de período 180º (π radianes).
- Dominio:
 (excepto π/2 + a · π), siendo a un número entero. O, con esta casuística: x ≠ ±π/2; ±3π/2; ±5π/2;…
(excepto π/2 + a · π), siendo a un número entero. O, con esta casuística: x ≠ ±π/2; ±3π/2; ±5π/2;… - Codominio:

- Derivada de la función tangente:

- Integral de la función tangente:

Cosecante

La cosecante es la razón trigonométrica recíproca del seno, es decir csc α · sen α=1.
La cosecante del ángulo α de un triángulo rectángulo se define como la razón entre la hipotenusa (c) y el cateto opuesto (a).

Su abreviatura es csc o cosec.
La gráfica de la función cosecante es:

La función de la cosecante es periódica de período 360º (2π radianes).
- Dominio:
 (excepto a · π), siendo a un número entero.
(excepto a · π), siendo a un número entero. - Codominio:

- Derivada de la función cosecante:

- Integral de la función cosecante:

Secante

La secante es la razón trigonométrica recíproca del coseno, es decir sec α · cos α=1.
La secante de un ángulo α de un triángulo rectángulo se define como la razón entre la hipotenusa (c) y el cateto contiguo o cateto adyacente (b).

Su abreviatura es sec.
La gráfica de la función secante es:

La función de la secante es periódica de período 360º (2π radianes).
- Dominio:
 (excepto π/2 + a · π), siendo a un número entero. O, con esta casuística: x ≠ ±π/2; ±3π/2; ±5π/2;…
(excepto π/2 + a · π), siendo a un número entero. O, con esta casuística: x ≠ ±π/2; ±3π/2; ±5π/2;… - Codominio:

- Derivada de la función secante:

- Integral de la función secante:

Cotangente

La cotangente es la razón trigonométrica recíproca de la tangente, por lo tanto tan α · cot α=1.
La cotangente de un ángulo α de un triángulo rectángulo se define como la razón entre el cateto contiguo o cateto adyacente (b) y el cateto opuesto (a).

Su abreviatura es cot, cotg o cotan.
La gráfica de la función cotangente es:

La función de la cotangente es periódica de período 180º (π radianes).
- Dominio:
 (excepto a · π), siendo a un número entero.
(excepto a · π), siendo a un número entero. - Codominio:

- Derivada de la función cotangente:

- Integral de la función cotangente:

Funciones definidas a trozos
Las funciones definidas a trozos (o función por partes) si la función tiene distintas expresiones o fórmulas dependiendo del intervalo (o trozo) en el que se encuentra la variable independiente (x).
Por ejemplo:


La imagen de un valor x se calcula según en que intervalo se encuentra x. Por ejemplo, el 0 se encuentra en el intervalo (-∞,1), por lo que su imagen es f(0)=0. El valor 3 está en el intervalo [1,4], entonces su imagen es f(3)=2.
Función derivada de una función
La función derivada f’ de una función f que sea derivable en un intervalo I es una nueva función que hace corresponder para cada valor de x ∈ I el valor de la derivada de f en ese punto.
En otras palabras, la función derivada f’ recoge todos los valores de las derivadas de f existentes en todos los puntos de su dominio.
Puede ocurrir que f no tenga derivada en todo su dominio. En ese caso, el dominio de la función derivada f’ es más pequeño que el dominio de f.
La expresión de la función derivada respecto a la función inicial es el siguiente límite:

La función derivada f’ de una función f, derivable en I, cuando el incremeto de la variable x ∈ I tiende a cero, es el cociente entre el incremento de la función inicial y el incremento de la variable independiente x.
Funciones inyectivas, sobreyectivas y biyectivas
La inyectividad, sobreyectividad y biyectividad dan información acerca de como se relacionan los elementos del conjunto inicial X con el conjunto final Y.
Cabe recordar que una función f es una relación que asigna a los elementos de un primer conjunto (conjunto inicial X) un elemento de un segundo conjunto (conjunto final Y).

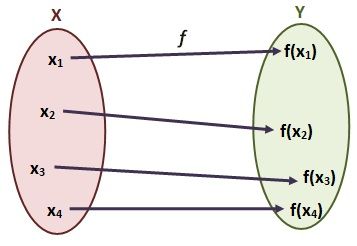
Función inyectiva
La función f es inyectiva si cada elemento del conjunto final Y tiene un único elemento del conjunto inicial X al que le corresponde. Es decir, no pueden haber más de un valor de X que tenga la misma imagen Y. Reciben también el nombre de funciones «uno a uno».
No siempre todos los elementos del conjunto final Y deben corresponderse con alguno del conjunto inicial X.

En términos matemáticos, una función f será inyectiva si dados dos puntos xa y xb:
Dicho de otra manera: una función es inyectiva si se cumple que a valores de su dominio x0 ≠ x1 ⇒ f(x0) ≠ f(x1).
Una comprobación gráfica de la inyectividad de una función es cuando cualquier recta paralela al eje X corta a la misma, como máximo, en un punto.
Función sobreyectiva
Una función f es sobreyectiva (o suprayectiva) si todo elemento del conjunto final Y tiene al menos un elemento del conjunto inicial X al que le corresponde.

Es decir, una función es sobreyectiva si el recorrido de la función es el conjunto final Y. Dicho de otra manera, una función es sobreyectiva cuando son iguales su codominio y su recorrido o rango.
Por lo tanto, también será sobreyectiva:

En términos matemáticos, una función f es sobreyectiva si:

Función biyectiva
Una función f es biyectiva si es al mismo tiempo inyectiva y sobreyectiva. Es decir, si todo elemento del conjunto final Y tiene al menos un elemento del conjunto inicial X al que le corresponde (condición de función sobreyectiva) y todos los elementos del conjunto inicial X tiene una única imagen en el conjunto final Y (condición de función inyectiva).
Digamos que no puede quedarse ningún elemento en el conjunto final Y solo, sin asociarse con un único elemento del conjunto inicial X.

Teóricamente, una función f es biyectiva si:
Funciones explícitas e implícitas
Una función explícita es aquella que está expresada de forma que la variable dependiente está despejada. Es decir, y = f(x).
Un ejemplo de función explícita sería:
Una función implícita es aquella que está expresada de forma que la variable dependiente y no está despejada. Es decir, que y no está definida en función solo de la variable independiente x.
Un ejemplo de función implícita sería:
Una función en forma implícita, despejando, siempre se puede pasar a la forma de una función explícita.
Función valor absoluto
La función valor absoluto devuelve el valor numérico del segundo término, pero afectado siempre del signo positivo. Tiene sentido para caracterizar distancias, longitudes.
La expresión más simple de una función valor absoluto es: f(x) = |x| y la gráfica son dos rectas simétricas en el primer y segundo cuadrante, con pendientes 1 y -1 (forma de “V”) que se cortan en el origen (0,0).

El dominio son números reales y el codominio, los reales positivos.
Una función valor absoluto se puede desplazar, simplemente, deslizándose el vértice a derecha e izquierda por el eje de las X con esta forma: f(x) = |x ±k|. (si k va con signo más , la gráfica se desplaza una distancia k hacia la izquierda; si k va con signo menos, la gráfica se desplaza una distancia k hacia la derecha). El vértice estará en (∓k, 0).

También se puede desplazar verticalmente, deslizándose el vértice arriba o abajo por el eje de las Y con esta forma: f(x) = |x|± k. (si k va con signo más, la gráfica se desplaza una distancia k hacia arriba; si k va con signo menos, la gráfica se desplaza una distancia k hacia abajo. El vértice estará en (0, ±k).

(En ambos casos, tomamos la constante k como un número positivo)

Por que resulta util el definirse una funcion a trozos para mofelar ciertos fenomenos
Porque describen el comportamientos de muchos fenómenos cotidianos
Cuáles son los nombres que recibe el dominio de una funcion ?
y=x^(2)+6 x-sqrt(16), como se el nombre de esta funcion?, oque tipo de funcion es. Y como se cual es el limite
Tu función en realidad, tal y como la planteas, podrían ser dos
y = x² + 6x ± √(16) = x² + 6x ± 4
Son polinómicas cuadráticas, o de segundo grado. No son ni inyectivas ni sobreyectivas, porque sus recorridos no coinciden con el dominio.
Gráfica, una parábola vertical abierta hacia arriba.
Por ejemplo, si planteas:
y = x² + 6x + 4
El recorrido es [- 5, +∞) y el dominio, los reales
y = x² + 6x – 4
El recorrido es [- 13, +∞) y el dominio, los reales
El límite es en un punto de la función.
Me prodrian ayudar indicando cuál es el dominio natural de la siguiente función r(x)=√ 5x-30 por favor.
Como se dice en la página:
Cuando el índice de la raíz n es par, el dominio de la función son los valores de x que hacen al radicando cero o mayor que cero.
5x – 30 >= 0
x >= 30 / 5 >= 6
Todos los números [6, + ∞) lo cumplen. Es el dominio.
Mira la página Dominio de una función en UNIVERSO FÓRMULAS
Hola no faltaria la funcion mantisa ?
Buenas tardes.
Me gustaría señalar un error en su definición de función sobreyectiva.
Cuando dicen que «Una función es sobreyectiva cuando son iguales su codominio y su dominio.», lo cual es falso. Creo que se referían a que <>
Gracias.
Sí. Evidentemente habrá habido una mala traslación del texto desde la pagina original Función sobreyectiva de UNIVERSO FÓRMULAS, donde textualmente se dice:
«cuando son iguales su codominio y su recorrido o rango.
Bién visto.
Hola me pueden ayudar esque quisiera saber qué clase de función es esta f(x)sin x+ cos x sería de gran ayuda
nose bro 😀
hola queria sacarme una duda, tengo esta tabla de valor y me pide que vea si es lineal, cuadrática o exponencial. la cosa que tuve 3 tabla de valor y dos coinciden a lo que estaba buscando pero esta no puedo saber cual es porque no coincide en ninguna y quiero sacarme la duda si estoy haciendo las cosas bien o pase algo en alto. si me podria sacar esta duda se lo agradeceria mucho
x y
0 1
1 2
4 16
6 64
Exponencial
f(x) = 2x
Buenas me gustaría saber, a ver si me pueden aclarar esta duda de que función es -8x+3
—
5
Función afín (UNIVERSO FÓRMULAS). Decreciente. Ordenada en orígen 3 (0, 3)
Hola, cual es el nombre de una funcion cuyo exponente esta elevado al cuadrado negativo?
es lo mismo los signos de positivo o negativo, lo que lo hace caudratica es que esta al cuadrado
Es una función radical. P.e.:
f(x) = 2 * x-2 = 2√(x).
me podrian ayudar con esto
T(t) = 20 − 2t; 0 t 8
Vuelve a escribirla, que no quedan claro los caracteres
yo no entiendo nada
Buenas noches,
me pueden indicar por favor que clase de funcion seria esta: f(x)=3-3/5 x+〖9/25 x〗^2
Muchas gracias
f(x)=3-3/5 x + 9/25 x^2
Corrijo 😀
Función polinómica racional, reductible a:
f(x) = (75x² – 15x + 9) / 25x²
Hola buenas noches quería saber que Nuncio es esta:
f(x)=(2x^2-4)/(x^2-4)
Función polinómica de cuarto grado.
muchas gracias por esta información
Excelente material, me fue de mucha ayuda
hola, me gustaría saber que clase de función es
y=2x+1
y=-x+2
y=x2
la función que a cada uno se le asocia su puesto (cual es su expresión algebraica)
la función que asocia el radio de una circunferencia a su perímetro (cual es su expresión algebraica)
Mira en esta página. Seguro que podrás clasificar cada función en los diversos tipos en los que encaja.
Es una función lineal
Muy buen aporte, me gustaría citar este trabajo, quizas podrían indicar como citar esta página
gracias me ayudo bastante con mi trabajo
Hola quería saber que clase de función son estas
F(x)=6
F(x)=5x^3
F(x)=3x
F(x)=x^2+2x-3
constante, cúbica, lineal, cuadrática
muy bueno el contenido, me fue y es de mucha ayuda como material didáctico.
Hola me gustaría saber que clase de función es esta ecuación: -2x+1-4y=0
Gracias.
Función polinómica de primer grado (y es función afín), expresada de forma implicita, porque y no está despejada.
una crítica: la parte de los corrimientos está totalmente mal. |x|+k sube la gráfica verticalmente, |x|-k la baja (asumiendo k positivo en ambos casos). Por otra parte, |x+k| corre la gráfica hacia la IZQUIERDA, mientras que |x-k| la corre hacia la DERECHA (de nuevo asumiendo k positivo en ambos casos).
Por ejemplo, cuando x=0, |x|+2 = 2, con lo que el vértice sube 2 unidades.
Otro ejemplo: cuando x=-2, |x+2|=0, con lo que el vértice se ha corrido 2 unidades hacia la izquierda.
Gracias por el apunte. Se han modificado los textos y las imágenes.
buenas esto me tiene ya calva estas preguntas limite de un radical limite de una derivada y limite de una forma infinito – infinito
Que bueno está esto gracias por subirlo me sirvió de mucho
Todo lo veo diferente casi no entiendo nada pero bueno necesito un profesor que sea bueno en matematicas porque no entiendo nada recien estoy aprendiendo algo
gracias muy útil
muy bueno para mi proyecto,me ayudo bastante
Gracias fue de mucha ayuda en mi clase
Muy bieno!
Gracias me ayudó mucho en mi consulta y adquirir más conocimientos de los tipos de funciones que existen
Lo importante es tu interés por saber.
Gracias me fue de mucha ayuda
el contenido es bueno pero no se puede imprimir lo que lo hace inutil por lo tanto lo considero malo e inutil
Botón derecho e imprimir.
En opción «`personalizado» eliges las páginas a imprimir.
UUSSSS QUE POCA PERSONA ES TIENES QUE TENER UNA IDEA DE COMO TRASCRIBIR YO LO PUEDE PASAR TODO QUE TAN TAN CONCHUDO QUIERE QUE SE LO HAGAN TODO O QUE MIJO
Clásico muchacho flojo, se debe leer es de información no para tu tarea
el típico Peresoso…así no se llega a ningún lado
Con todo respeto no me convence la gráfica de la función cúbica pues los (-1)^3= -1, (-2)^3=-8, (-3)^3= -27.
Ten en cuenta que la gráfica es de un ejemplo cualquiera de función cúbica.
En la página se dice:
Una función cúbica puede tener tres raíces reales dos o una
La que tu sugieres:
f(x) = x³
tiene una raíz, x = 0
gracias es bueno aprender algo nuevo
los amo me salvaron la vid
buena explicacion felicidades
muchas gracias me ayudo mucho su informacion sigan asi , buen trabajo, y nuevamente gracias…..
Si es un tema que se debe aprender, pero recomiendo que expliquen con más ejercicios, que ocurre si no sale una respuesta, que tipos de gráficas puede tener y además una explicación más detallada con los pasos para saber cómo se hace. (0_0)