
Una parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco y de una recta fija del mismo plano llamada directriz.

La parábola es una sección cónica, resultado de la intersección de un cono recto con un plano que corta a la base del mismo, oblicuo a su eje y paralelo a una generatriz g de la superficie cónica.
El foco y la directriz determinan cómo va a ser la apariencia de la parábola (en el sentido de que «parecerá» más o menos abierta según sea la distancia entre F y la directriz). Todas las parábolas son semejantes. Su excentricidad es 1 en todos los casos. Solamente varía la escala.

Una de las aplicaciones físicas más importantes de la parábola es el movimiento parabólico. Este movimiento se caracteriza porque una partícula o cuerpo sólido lanzado en un campo gravitatorio recorre una trayectoria parabólica.
Una aplicación práctica de la parábola son las antenas parabólicas, en las que todas las rectas paralelas al eje de la cónica se reflejan en el foco de la misma. (Empleado en óptica, antenas de transmisión de radiofrecuencia, estufas domésticas parabólicas, captación de energía solar, etc.).
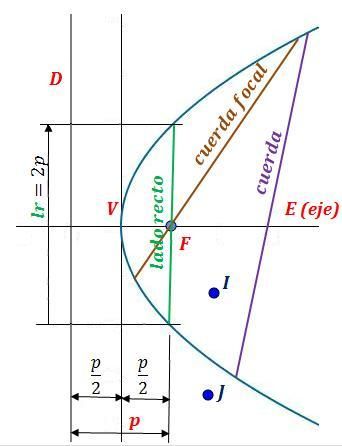
Elementos de una parábola
Los elementos de la parábola son:

- Foco: el foco F es el punto fijo. Los puntos de la parábola equidistan del foco y la directriz.
- Directriz: es la recta fija D. Los puntos de la cónica equidistan de la directriz y el foco.
- Radio vector: es el segmento R que une el foco con cada uno de sus puntos. Es igual al segmento perpendicular a la directriz desde el punto correspondiente.
- Eje: es la recta E perpendicular a la directriz que pasa por el foco y el vértice. Es el eje de simetría de la parábola.

- Parámetro: p es la distancia entre el foco y el punto más próximo de la directriz.
Es importante el signo que lleve el parámetro en la ecuación. En las parábolas verticales, cuando el parámetro lleva signo positivo la cónica se abre hacia arriba. Cuando el signo de p es negativo, ésta se abre hacia abajo. Igualmente, en las parábolas horizontales, cuando el signo que lleva p es positivo, se abre hacia la derecha y cuando el signo que lleva p es negativo, la cónica se abre a la izquierda.
(Algunos autores llaman parámetro a la distancia entre foco y vértice).
- Vértice: es el punto V de la intersección del eje y la parábola.
- Distancia focal: distancia entre el foco F y el vértice V. Es igual a p/2.
- Puntos interiores y exteriores: la parábola divide el plano en dos regiones. Los puntos que están en la región del foco se llaman puntos interiores (I), mientras que los otros son los exteriores (J).
- Cuerda: segmento que une dos puntos cualesquiera de la cónica.
- Cuerda focal: una cuerda que pasa por el foco F.
- Lado recto: Cuerda focal paralela a la directriz D y, por tanto, perpendicular al eje E. Su longitud es dos veces el módulo del parámetro (2p, pues se ven en la figura dos cuadrados unidos iguales de lado p).
(Debe recordarse que entre foco, vértice y directriz, el vértice V está siempre en el centro. El orden es F – V – D o D – V – F).
En una parábola de eje vertical con su ecuación cuadrática expresada en forma estándar:
La ecuación del eje es:

Las coordenadas del vértice sobre los coeficientes de la misma forma de ecuación son:

Excentricidad de la parábola

La parábola es la única de las cónicas cuya excentricidad es siempre 1.
Veamos la figura.
Por la misma definición de parábola, su excentricidad siempre es la unidad. De esto deriva que todas ellas sean semejantes, variando su apariencia de cerradas o abiertas, según la escala.
Ecuación de la parábola
La ecuación de la parábola depende de si el eje es vertical u horizontal. Si el eje es vertical, la y será la variable dependiente y tendrá un término en x². Si el eje es horizontal, será x la variable dependiente y tendrá un término en y².
Ecuación ordinaria reducida

Consideremos una parábola de la imagen de arriba. Es horizontal (cuyo eje es el X de las abscisas), su vértice está en el centro de coordenadas V (0, 0) y que la parábola está en la parte positiva de las x. En este caso, el foco estará necesariamente en F (p/2,0), a la derecha del vértice. La ecuación de la recta directriz D será x = –p/2, porque la directriz y el foco equidistan del vértice.
Los radios vectores FP y PM, correspondientes a cualquier punto P de la parábola (que, por definición de la misma, son iguales) tendrán la longitud:

Operando y simplificando, obtenemos la ecuación ordinaria o canónica reducida de la parábola referida a esta configuración:
Que es la de la parábola horizontal con vértice en (0, 0) y abierta a la derecha, como se muestra en la gráfica de arriba.
(Cabe decir que la ecuación de una parábola horizontal se corresponde con dos funciones. Despejando la variable dependiente y).

Se ve en la imagen que la solución positiva de la raíz cuadrada es la función cuya gráfica es la media parábola de arriba mientras que la solución negativa es la función de la media de abajo.

Volviendo a la ecuación ordinaria reducida de la parábola horizontal. Si se desplazara el vértice a un punto V(xv, yv), tendríamos la ecuación canónica en forma vértice o ecuación ordinaria de la cónica horizontal. Se escribirá así:
Como se ve en la imagen. Está también la ecuación de la recta directriz D:

Vamos a la ecuación ordinaria reducida de la parábola, pero ahora con su eje vertical y coincidente con el eje de las ordenadas, su vértice es el centro de coordenadas V (0,0) y está en la parte positiva de las y (abierta hacia arriba).

Esta ecuación ordinaria o canónica reducida vertical se deduce con el mismo procedimiento empleado en la reducida horizontal, es decir, a partir de operar sobre la igualdad de los radios vectores de cualquier punto P(x,y).
Ahora, si se desplazara el vértice de la parábola vertical a un punto V(xv, yv), tendríamos la ecuación ordinaria en forma vértice de la parábola vertical o ecuación canónica. Se escribirá así:
En la imagen está también la ecuación de la recta directriz D:

Análogamente, vemos las expresiones de la ecuación ordinaria o canónica reducida para las parábolas con ejes coincidentes con el eje de las abscisas o con el eje de las ordenadas, siempre con el vértice en el origen V (0,0), pero ahora con valores negativos de las x y de las y respectivamente. Se muestra en las dos imágenes siguientes:
Ecuación canónica reducida de la parábola horizontal abierta a la izquierda:

Ecuación canónica reducida de la parábola vertical abierta hacia abajo:

Otras ecuaciones
La ecuación canónica u ordinaria de la parábola vertical con vértice V (xV,yV) se puede transformar en la ecuación cuadrática en forma estándar:

En la que las constantes tienen el siguiente valor:

Donde a ≠ 0 y b y c son números reales.
Lo vemos en la imagen:

La ecuación del eje es:

Las coordenadas del vértice sobre los coeficientes de la misma forma de ecuación son:

La parábola cortará el eje de ordenadas en el punto (0,c).
La constante a indica lo “abierta” que es la parábola. Cuando el valor de a es menor, aparecerá más abierta. Dicho de otra manera, la parábola aparecerá más abierta cuando el parámetro p sea mayor. Si la constante a es positiva, el vértice V será el mínimo de la cónica, es decir, se abre hacia arriba. Si la constante a es negativa, el vértice V será máximo de la parábola, o sea, que se abre hacia abajo.
Unas parábolas verticales:

Igualmente, la ecuación canónica u ordinaria de la parábola horizontal con vértice V(xV,yV) se puede transformar en la ecuación cuadrática en forma estándar:

En la que las constantes tienen el siguiente valor:

Al igual que en la parábola vertical, la constante a indica lo “abierta” que es ésta. Cuando el valor de a es menor, la cónica aparecerá más abierta. Dicho de otra manera, la parábola aparecerá más abierta cuando el parámetro p sea mayor. Si la constante a es positiva, la parábola se abre hacia la derecha. Si la constante a es negativa, se abre hacia la izquierda.
Ya se ha dicho que todas las parábolas tienen excentricidad e = 1, por lo que son semejantes, variando su apariencia de cerradas o abiertas.

Es importante el signo que afecta al parámetro p. En las parábolas verticales, cuando el signo del parámetro es positivo ésta se abre hacia arriba. Cuando el signo de p es negativo, la parábola se abre hacia abajo. Igualmente, en las parábolas horizontales, cuando el signo de p es positivo, se abre hacia la derecha y cuando el signo de p es negativo, se abre a la izquierda.
En este cuadro se muestran las cuatro configuraciones de parábolas horizontales o verticales con el vértice en el origen V(0,0):

Ecuación general de la parábola
Los casos anteriores donde el eje es vertical u horizontal, son casos particulares de la parabola, porque el eje puede ser oblícuo.
Todas las posiciones que pueda adoptar una parábola están representadas por la ecuación general de la parábola:

Veamos casos de la parábola inclinada o parábola oblicua.

En estos cuatro casos su ecuación tiene todos los términos de la ecuación general.
Se puede comprobar que en las cuatro parábolas se cumplen las dos condiciones de la ecuación general de la parábola, es decir que B2 – 4AC = 0 y que A y C no son nulos al mismo tiempo.
La Ecuación general tiene estos dos casos particulares:
- Ecuación general de la parábola con el eje vertical
La ecuación general queda reducida a estos términos cuando se refiere a la parábola vertical:

De la ecuación ordinaria de la parábola vertical:

Se pasa a su ecuación general desarrollando el cuadrado del binomio, agrupando los términos y ajustando la correspondencia de coeficientes:

- Ecuación general de la parábola con el eje horizontal
La ecuación general queda reducida a estos términos cuando se refiere a la parábola horizontal:

Por el mismo procedimiento que en la parábola vertical, los coeficientes de la ecuación general tienen estas equivalencias:

Nota. No confundir los coeficientes A, B, C, D, E y F de la ecuación general de la parábola (en mayúsculas) con los coeficientes a, b y c de la ecuación cuadrática en forma estándar de la parábola (minúsculas).
Raíces de una parábola
Las raíces de una parábola vertical de ecuación son los puntos de la misma de ordenada nula (y = 0), es decir, allí donde la parábola corta al eje de ordenadas OX.
Una parábola vertical puede tener dos raíces, una o ninguna.
Como en el corte con OX, y = 0, los puntos de cortes serán las raíces de una ecuación de segundo grado (función cuadrática):
Cuyas raíces se hallan por la fórmula:

Donde el binomio que se halla dentro de la raíz cuadrada es el que determina el número de raíces de la parábola.

Los tres casos y la aplicación del criterio se ilustra en estas tres parábolas:

Así, en el caso de dos raíces, podemos hacer este desarrollo:

Por el punto medio de las dos raíces pasará el eje de la parábola, su eje de simetría. El resultado coincide con el hallado para ordenada del vértice de una parábola vertical.
Si ésta tuviese una raíz, la ordenada del vértice será el valor de la misma raíz y, por tanto, la ecuación del eje de la parábola:
A partir de aquí, la ecuación de la parábola vertical se puede expresar también así:
La parábola vertical cortará al eje OY cuando la ordenada sea nula, cuando x = 0.

Vértice de una parábola
El vértice de una parábola V es el punto donde ésta corta a su eje.
Hemos visto que la ecuación cuadrática en forma estándar de la parábola vertical se puede deducir de la ecuación canónica u ordinaria.
Si a las coordenadas del vértice les llamamosV (xV, yV), la transformación es:

De la igualdad 1) de arriba se deduce el coeficiente b de la igualdad 2). Si en esa equivalencia sustituimos el valor del parámetro p que se obtiene del coeficiente a, tenemos la abscisa del vértice, xV:

El término libre de 1) será igual al término libre c de la igualdad 2) y sabemos el valor de p en función de a:

En la primera igualdad se sustituyen los valores de xV y de p, simplificando la expresión:

Se despeja y, pasando de una fracción mixta a común denominador, llegamos a la expresión de la ordenada del vértice de la parábola en función de los parámetros de la ecuación cuadrática en forma estándar de la parábola vertical:

El resultado lo vemos en la imagen:

La parábola vertical podía igualmente expresarse mediante la ecuación general.
A partir de esa ecuación se deducen las coordenadas del vértice mediante las expresiones:

Tangente a la parábola

Las rectas tangente y normal a cualquier punto P de una parábola son las bisectrices de los ángulos formados por los radios vectores correspondientes a ese punto. De las dos bisectrices, hay que tener en cuenta cuál es la tangente y cuál la normal.
Las dos tangentes que pasan por los extremos del lado recto son perpendiculares entre sí y se cortan en la intersección de la directriz con el eje. Con este último forman dos ángulos de 45°.

Ejercicios resueltos
Ejercicio 1
Hallar la ecuación de la parábola cuyo eje es paralelo al eje de las abscisas OY, que pasa por el punto P (4,0) y su vértice está en V (2,-1).
Hacer su representación gráfica.
Solución:
Como el eje de la parábola E es paralelo al eje OY, la ecuación será del tipo:
Sustituyendo las coordenadas del vértice en la ecuación:
Sabemos que la parábola pasa por P (4,0), luego:

Ésta es la ecuación buscada. Como la ordenada del vértice es 2, la ecuación del eje de la parábola, paralelo a OY será x = 2.
Finalmente, como hemos averiguado el parámetro p = 2, la recta directriz, que es perpendicular al eje E y paralelo al eje de ordenadas OX, estará a p/2 del vértice, luego su ecuación será y = -1 –p/2 = -2.
El resultado del ejercicio lo vemos en la imagen:

Ejercicio 2
La ecuación de una parábola es y2 = 6x -3. ¿Cuáles serán las ecuaciones de las rectas tangente y normal de ordenada en un punto P de la parábola x = 6,5 y ordenada positiva?

Solución:
Las ordenadas para una abscisa x = 6,5 serán:

Tomaremos yP = +6, pues la ordenada tiene que ser positiva, según el enunciado.
Por tanto, las coordenadas del punto de tangencia serán: P (6,5, 6).
La ecuación de este ejercicio se puede transformar en:

Recordemos que es una parábola horizontal, cuya ecuación general es:

En la que las constantes hemos visto que tienen el siguiente valor:

El parámetro p se puede hallar por la fórmula del coeficiente a de la variable al cuadrado de una parábola:

La abscisa yV del vértice V es la siguiente:

La ordenada xV del vértice V es la siguiente:

Las coordenadas del vértice serán: V (1,5 , 0).
Como la abscisa del vértice yV = 0, el eje E y el foco F están sobre el eje OX.
Por lo tanto, la abscisa del foco F será:

Y las coordenadas del foco F (2, 0).
La recta del radio vector FP la obtenemos por la fórmula de la recta que pasa por dos puntos:

La ecuación de la recta perpendicular a la directriz D desde el punto P es x = 6.
Con las ecuaciones de los radios vectores, podemos aplicar la ecuación de la bisectriz, que serán las ecuaciones de la tangente y la normal a la parábola del ejercicio en el punto P (6,5 , 6).

Como la tangente tiene pendiente positiva, se emplea el signo positivo “+”.

La recta normal en P tiene pendiente negativa, por lo que se emplea el signo “-“.

El resultado aparece en esta imagen:

Ejercicio 3
Hallar la ecuación de una parábola vertical abierta hacia arriba, sabiendo que las coordenadas de su vértice son V (2,-1) y la de uno de sus puntos P (-2,3).

Solución:
Si la parábola es abierta hacia arriba, sabemos que su vértice es el mínimo de ésta.
Además, si la parábola es vertical, su ecuación se puede escribir de la forma:
Para que un punto de una función sea un máximo o un mínimo, debe cumplirse que su derivada sea nula. La derivamos y la igualamos a cero:
Asignándole las coordenadas del vértice, que es un mínimo de la parábola, a la derivada:

Despejamos b:
Vamos a sustituir los valores de las coordenadas de los dos puntos conocidos, V (2,-1) y P (-2,3) en la ecuación (Ec 1):

Operando:

Sustituimos b de la (Ec 2) en las ecuaciones (Ec 3) y (Ec 4).

De estas dos últimas ecuaciones, restamos miembro a miembro la segunda de la primera:

Sustituimos el valor hallado de a en la (Ec 2):

Y, por fin, los valores de a y b:

Asignamos el valor de las constantes a, b y c a (Ec 1) y tenemos la ecuación de la parábola que buscábamos.


Ejercicio 4
Conocemos de una parábola dos puntos, M (-4,-8) y N (8,-8) y su parámetro p = -2. Hallar las coordenadas de su vértice y la ecuación.
Solución:
Como yM = yN = -8, se trata de una parábola de eje vertical.
El parámetro es negativo, por lo que se trata de una parábola abierta hacia abajo, como se ve en la figura:

La ecuación de la parábola vertical es:
Sustituimos en esta ecuación (Ec 1) sucesivamente las coordenadas de M y N:
Y, ahora, las coordenadas de N:
Como los dos segundos términos son iguales, igualamos los primeros términos de las dos ecuaciones (Ec 2) y (Ec 3):

Sustituimos este valor en cualquiera de las dos ecuaciones anteriores, por ejemplo en(Ec 4):

Las coordenadas del vértice son: V(2, 1).
Sustituimos las coordenadas del vértice halladas en la ecuación (Ec 1).

Que es la ecuación buscada de la parábola.

Ejercicio 5
1. Determinar las coordenadas del vértice y el foco.
2. Las longitudes del parámetro y del lado recto.
3. Las ecuaciones del eje de la parábola y de su recta directriz, todo de una parábola, cuya ecuación en forma general es:
Solución:
Como el término que está al cuadrado es el de x2, se trata de una parábola vertical.
Se modifica la ecuación general para llegar a la forma ordinaria o canónica en forma vértice, del tipo:
Agrupar los términos en x, dejando el resto a la derecha:
Buscando formar el cuadrado de un binomio, se añade el cuadrado del número necesario a derecha e izquierda de la igualdad, en este caso 2², el 4:
Se puede formar a la izquierda de la igualdad el cuadrado de un binomio, apareciendo, en la forma adecuada, la ecuación canónica u ordinaria de la parábola en forma vértice:

De aquí se desprenden, si se consulta la expresión puesta en la forma canónica u ordinaria, las coordenadas del vértice y la dimensión del parámetro. El doble de p es el lado recto:

Como el signo del segundo término de la igualdad es negativo, se trata de una parábola vertical abierta hacia abajo. Por tanto, su eje, que pasa por el vértice de abscisa xV = 2, será una recta vertical con ecuación:
Arriba del vértice estará la recta directriz a una distancia p/2 = 2/2 = 1 sobre la ordenada del vértice yV, por lo que la ecuación de la recta directriz será:

Finalmente, las coordenadas del foco, situado sobre el eje y por debajo del vértice, también a una distancia p/2 = 2/2 = 1, serán:

Los resultados del ejercicio se muestran en la imagen:

Ejercicio 6
Hallar la ecuación de la parábola vertical que pasa por los puntos P1 (-1,7), P2 (2,4) y P3 (3,11).
Solución:
Como es una parábola vertical, su ecuación cuadrática en forma estándar será en x², en la forma:
Esta ecuación debe cumplirse para los tres puntos por los que pasa la parábola:

Operando, nos queda un sistema de tres ecuaciones lineales con tres incógnitas:

Se resuelve el sistema, por cualquiera de los métodos, como reducción, sustitución o determinante de Gauss, que aquí no se desarrollará. La solución del sistema es:

Por lo tanto, la ecuación de la parábola será:
Se ve en la figura:

¿Sabías que?
Una propiedad de la parábola, conocida desde hace dos milenios ha dado lugar a muchas aplicaciones prácticas, que encontramos en la vida cotidiana.
Pero recordemos el fundamento matemático de esta cónica puesto más arriba:
Una parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo, llamado foco y de una recta fija del mismo plano llamada directriz.
Se representa en la figura:

La parábola, girando sobre su eje 360° da lugar a una superficie tridimensional llamada paraboloide.
Las antenas parabólicas, los radiotelescopios o los faros de los coches, se basan en esta propiedad (que aquí se aplica sobre un paraboloide).
Las señales radioeléctricas, haces de luz, ondas electromagnéticas, que se emiten desde el foco y rebotan en la superficie de la antena, salen al exterior paralelas al eje. En sentido contrario, la antena recibe del exterior las señales paralelas al eje, rebotan en la superficie y se concentran en el foco.


Nmms tengo que escribir todo
Hay comentarios como no es correcta en general considero que hizo un gran esfuerzo y puede tranquilamente escribir p p/2 . Por otro lado no es ninguna colaboración decir no son correctas, sino en caso de ser no correctas deben de dar la corrección y eso si es una colaboración. Sino simple es una critica sin colaboración.
Buen comentario, Luís.
Por ejemplo:
«depende de considerar el parámetro p como la distancia del foco al punto más próximo a la directriz (criterio que se sigue en esta web) o que el parámetro, como definen otros autores, sea la distancia entre el foco y el vértice.
Las ecuaciones correctas para el estudio inicial de las parábolas que describo son para vértice en el origen, donde p es la distancia del vértice de la parábola al foco.
y^2=4px
x^2=4py
Donde precisamente 4p es la longitud del lado recto.
Tus ecuaciones y las de esta página son correctas. Pero depende de considerar el parámetro p como la distancia del foco al punto más próximo a la directriz (criterio que se sigue en esta web) o que el parámetro, como definen otros autores, sea la distancia entre el foco y el vértice.
Como se saca el área de una conica parabola
Una parábola es una cónica.
Quieres la superficie de revolución al girar una parábola o el área comprendida en el plano dentro de la parábola, siempre entre un intervalo?
Que tal, puedo ver que le invertiste mucho tiempo a tu articulo y se agradece , solo una observación , al parecer manejas información que no es correcta, si me permites te invito a que revises bien tu información y lo corrijas para que mayor cantidad de personas se puedar apoyar con tu información.
Saludos y felicitaciones por tu entusiasmo.
Inquietud para cualquiera que desee colaborar, en especial si es Ingeniero o estudia Ingeniería Civil: En un video que ví en YouTube , y en un tema sobre áreas donde se usa la parábola el ponente dice : » En una parábola , la altura H ( entiéndase desde el vértice a un punto cualquiera en la curva), es directamente proporcional al cuadrado de la mitad de la base B ( la base es la distancia o abertura total d la parábola). Esto sirve para corte de hierro en vigas.
Les comento que hice ejercicios y se cumple lo anterior, pero he buscado por todos lados bibliografía sobre esta propiedad de la parábola y no he encontrado. Si alguien tiene algo favor publicar.
hay información errónea
quien es el autor???????
las referencias porfis la bibliografia
Si tienes solamente dos puntos, sin ningún dato más, no puedes hallar la ecuación de la parábola.
si esos puntos son el vertice y el foco si se podría
Se entiende que son dos puntos pertenecientes a la parábola sin ninguna especificación más. Se podría calcular conociendo un punto cualquiera y se especificasen las coordenadas del vértice, siempre que la parábola fuese vertical, es decir, con el eje paralelo a OY
tengo una pregunta ¿como podría yo encontrar la parábola diagonal (aquella que su valor es X=Y), no encuentro la formula, pero entiendo que se crea una linea llamada «Z», si estoy mal, por favor díganme, me confunde un poco ese pedazo
Una pregunta, esto sirve para instalar una antena parabolica en la circuncision estatal que morgan freeman estudio cuando se creo la Tierra?
perfecto
Las funciones que están en las gráficas no coinciden con las gráficas.
TODO BIEN ENTENDIDO Y FASIL DE COMPRENDER
que interesante
mi estimado, creo que esta mal nominado la ecuación en los gráficos.