Elipse

¿Qué es una elipse?

La elipse es el lugar geométrico de los puntos del plano cuya suma de las distancias a los dos focos (puntos interiores fijos F₁ y F₂) es constante. Es decir, para todo punto a de la elipse, la suma de las distancias d₁ y d₂ es constante.

También podemos definirla como una cónica, consecuencia de la intersección de un cono con un plano oblicuo que no corta la base.

• Elementos
• Ecuación
  • Ecuación ordinaria
  • Ecuación paramétrica
  • Ecuación general
• Área
• Perímetro
• Excentricidad
• Tangente a una elipse
• Ejercicios resueltos

Elementos de una elipse

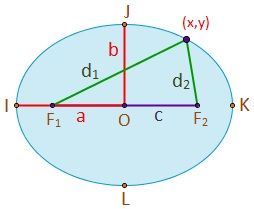
Los elementos más importante de la elipse son:

• Focos: son los puntos fijos F₁ y F₂ que generan la elipse. La suma de las dos distancias de cualquier punto a los dos focos (d₁ y d₂) es constante.
• Distancia focal (2c): distancia entre los dos focos. F₁F₂=2c. c es la semidistancia focal.
• Centro: es el punto medio de los dos focos (O).
• Semieje mayor: longitud del segmento OI o OK (a). La longitud es mayor a la del semieje menor. La suma de las distancias de cualquier punto de la cónica a los focos es constante y ésta es igual a dos veces el semieje mayor:
  

  (La constante de la elipse es precisamente la longitud 2a).

• Eje focal o principal: es la recta que pasa por los focos, el centro y también por dos vértices. Es uno de los ejes de simetría de la elipse. En él está el segmento 2a.



• Semieje menor: longitud del segmento OJ o OL (b). Ambos semiejes cumplen que:
  

  Como vemos en el dibujo, esta relación cumple el teorema de Pitágoras.

• Eje normal o secundario: es la recta que pasa por el centro de la elipse y es perpendicular al eje focal. Es el segundo de los ejes de simetría de la cónica. En él está el segmento 2b. El eje principal y el eje normal son los dos ejes de simetría.
  
• Radios vectores: los radios vectores de cualquier punto (P=(x,y)) son los dos segmentos que lo unen con los dos focos. PF₁ y PF₂ (en el dibujo, d₁ y d₂).
• Vértices: son los puntos resultantes de la intersección de la elipse con la recta que pasa por los focos (eje focal), F₁F₂, y su perpendicular que pasa por el centro (eje normal). Es decir, son los puntos I, J, K y L
• Lado recto (LR): es el segmento perpendicular al eje principal que, pasando por un foco, une dos puntos de la elipse. Su longitud es:
  

Ecuación de una elipse

Los puntos pertenecientes a la elipse (x, y) son los puntos del plano que cumplen que la suma de su distancia a los dos focos es constante.

Existen diferentes ecuaciones de la elipse, que veremos a continuación:

Ecuación ordinaria o canónica de la elipse

A partir de la propiedad de la elipse, que es que la suma de la distancia de cualquier punto a los focos (los radios vectores) es igual a 2a, en una elipse horizontal (de eje focal paralelo al eje de las abscisas X) y el centro situado en un punto O (o₁, o₂):

Se llega a la ecuación ordinaria o canónica de la elipse:

En el caso de que esta cónica, también horizontal, esté centrada en (0, 0), la ecuación ordinaria reducida es:

Si el eje principal fuese paralelo al eje de las ordenadas OY:

La ecuación ordinaria de esa elipse vertical con centro en el punto (o₁, o₂) se convierte en:

Igualmente, una elipse vertical con el centro coincidente con el centro de coordenadas (0, 0).

Su ecuación ordinaria se convertiría en:

Fácilmente se puede apreciar cual es el semieje mayor, viendo cuál de las incógnitas lleva el denominador mayor.

Ecuación paramétrica de la elipse

A partir de una elipse horizontal con centro en O (o₁, o₂) y semiejes a y b, se trazan dos circunferencias de radios también a y b.

Un segmento cualquiera OQ, que corta a la circunferencia menor en P, forma un cualquiera t con el semieje positivo de las abscisas.

A la vista de la imagen, la abscisa del punto Q coincidirá con la de un punto X.

De la misma manera, la ordenada del punto P será la misma que la del punto X.

Podemos plantear las ecuaciones paramétricas:

Si la elipse horizontal está centrada en el origen de coordenadas (0, 0), sus ecuaciones paramétricas se simplificarán.

La misma construcción geométrica se aplicará en el caso de una elipse vertical, cuyo centro esté en el origen de coordenadas (0, 0).

Aquí, las ecuaciones paramétricas serán.

Ecuación general de la elipse

Desarrollando los cuadrados de los numeradores de la ecuación ordinaria, eliminando denominadores y simplificando, se llega a la ecuación general de la elipse, que en su forma extensa es la ecuación general de las cónicas:

Para que estos coeficientes se correspondan con una elipse, tiene que cumplirse que A y C deben ser los dos positivos (el mismo signo).

Si los dos ejes son paralelos a los ejes de coordenadas, se cumple también necesariamente que:

En estos dos casos de elipse horizontal o vertical, no está presente en la ecuación general el término Bxy:

Si el eje principal es paralelo al eje de abscisas (elipse horizontal), A debe ser menor que C.

Si el eje principal coincide con el de abscisas, además E = 0.

Si el centro de la elipse horizontal está en el origen de coordenadas:

Y, al contrario, si el eje principal es paralelo al eje de ordenadas (elipse vertical), C debe ser menor que A:

Cuando una elipse vertical tiene el eje coincidente con el de las ordenadas, además D = 0. Y, si además ésta tiene su centro en el origen de las coordenadas, D = 0 y E = 0.

Cuando la elipse está rotada o inclinada (los ejes no son paralelos a los coordenados) ha de existir el término Bxy:

Solamente cuando la rotación es tal que el eje principal es paralelo a las bisectrices de los cuadrantes de los ejes coordenados, entonces A = C:

Y debe de cumplirse:

Condición que es general para toda elipse.

Las equivalencias de los coeficientes de la ecuación general en una elipse horizontal son:

Y las de una elipse vertical:

Área de una elipse

El área comprendida dentro de una elipse es π veces el producto de los dos semiejes (a y b).

En el caso de que los dos semiejes fuesen iguales (r=a=b), se trataría de una circunferencia. Y la fórmula del área de la elipse se convertiría en la del área comprendida dentro de una circunferencia (o lo que es lo mismo, el área del círculo):

Perímetro de una elipse

El cálculo del perímetro de la elipse (o longitud de la elipse) es muy difícil, aunque no lo parezca. Requiere de integrales complicadas para su cálculo. Existen fórmulas que aproximan el cálculo hasta valores bastante exactos. Existe una aproximación con menos del 5% de error, siempre que el semieje mayor (a) no sea mucho más grande que el menor (b):

El matemático Ramanujan dio una aproximación más exacta que la anterior:

El mismo Ramanujan mejoró la aproximación con la llamada fórmula Ramanujan II:

Donde el parámetro H se halla así:

Esta buena aproximación disminuye ligeramente cuando la excentricidad e tiende a 1 (a una elipse plana).

La fórmula Ramanujan II, con la corrección Ramanujan II-Cantrell quedó optimizada para conseguir una aproximación muy alta para todo el rango de e, corrigiendo la pequeña desviación que se producía cuando la elipse era muy achatada (e → 1).

El error máximo de esta última fórmula es un sorprendente 0,00145%.

El valor exacto nos lo puede dar la fórmula de Gauss-Kummer. Es una serie infinita que se obtiene mediante un cálculo diferencial complicado cuyo desarrollo rebasa los objetivos de esta web.

Con tal sólo los cuatro o cinco primeros términos de la serie, se obtiene un resultado con una aproximación muy alta.

En los tres cuadros siguientes se ve el resultado, con seis decimales, de tres de las fórmulas ofrecidas: la primera aproximación, la de Ramanujan en su versión Ramanujan II y la fórmula Ramanujan II-Cantrell.

En cada cuadro se estima el perímetro de una elipse, cubriendo entre las tres imágenes todo el rango de la excentricidad: 0 ≤ e ≤ 1.

Se concluye que si la elipse tiende a una circunferencia, es decir cuando e → 0, puede usarse la primera fórmula por su facilidad y sencillez, siempre que no se persiga una gran exactitud.

Para una excentricidad intermedia e, pueden usarse las dos fórmulas de Ramanujan.

Cuando estamos ante una elipse con una excentricidad alta, o sea, si e → 1 (tiende a una elipse plana), la mejor alternativa es la fórmula Ramanujan II-Cantrell.

Excentricidad de la elipse

La excentricidad de una elipse (e) es un valor que determina la forma de la elipse, en el sentido de si es más redondeada o si se aproxima a un segmento. Sea c la semidistancia focal y a el semieje mayor:

La excentricidad puede tomar valores entre 0 y 1 (0 < e < 1). Tiende a 0 cuando la elipse tiende a una circunferencia. En este caso el semieje menor tiene a igualarse al mayor y los focos (F₁ y F₂) tienden a confundirse con el centro de la elipse. Cuando la excentricidad crece y tiende a 1, ésta se aproxima a un segmento.

Existe otra fórmula que calcula la excentricidad a partir de los dos semiejes (a y b).

Esta fórmula se obtiene a partir de la anterior ya que se cumple que:

En la imagen se muestran varias excentricidades comparadas:

Tangente a una elipse

La ecuación de la recta tangente a una elipse, horizontal y centrada en el origen de coordenadas, en uno de sus puntos P(x_P, y_P):

Viene dada por la ecuación:

O por esta ecuación equivalente:

La recta normal a este tipo de elipse en uno de sus puntos P, que por rectas perpendiculares, tendrá una ecuación de una recta también perpendicular a la recta tangente:

Como en la imagen:

Igualmente, si la elipse es vertical y también centrada en el origen de coordenadas, las ecuación de las rectas tangente y normal en uno de sus puntos P(x_P, y_P) serán:

En el caso de que el eje focal sea paralelo al eje de las abscisas (elipse horizontal) y tenga su centro O (o₁, o₂) desplazado del origen de coordenadas O(0, 0), la ecuación de la tangente en uno de los puntos P (x_P, y_P) es la siguiente:

Como en la imagen:

Ejercicios

Ejercicio 1

Las ecuaciones paramétricas de una elipse son:

Hallar:

a) Los dos semiejes a y b.

b) Las coordenadas del centro O (o₁, o₂).

c) La distancia focal 2c y las coordenadas de los focos F₁ y F₂.

d) Las coordenadas de los cuatro vértices I, J, K y L.

e) La longitud del lado recto LR.

Solución:

Transformamos las ecuaciones paramétricas para llegar a la ordinaria:

Este último paso mediante la identidad fundamental de la trigonometría. Y llegamos a la formulación canónica u ordinaria de una elipse horizontal con el centro desplazado del origen de coordenadas:

a) A la vista de esta ecuación, los semiejes son:

b) Las coordenadas de su centro:

c) La distancia focal 2c y las coordenadas de los focos F₁ y F₂ se obtienen, la primera a través del teorema de Pitágoras:

Las coordenadas de los focos se obtienen, sabiendo que estos están sobre el eje principal o focal, de ecuación y = -7, y conocemos el semieje a = 10:

d) Las coordenadas de los cuatro vértices I, J, K y L se obtienen sumando o restando el largo de los semiejes a y b de las coordenadas del centro de la elipse, como se ve en la figura:

c) La longitud del lado recto LR.

El mismo resultado se puede obtener de la diferencia de las ordenadas de los extremos del lado recto, en su intersección con la elipse. Estas ordenadas se pueden obtener de la ecuación, dándole a la x el valor de la abscisa de uno de los focos, por ejemplo del F₂, con abscisa 20.

En la imagen:

El lado recto es de 7,2.

Ejercicio 2

Sea una elipse de centro O=(4,-2) y de semiejes a=3 cm y b=2 cm. La ecuación de ésta es:

Ejercicio 3

Tenemos una elipse, con el centro O en el origen de coordenadas, cuya ecuación es:

Encuentra sus focos, los cuatro vértices y su excentricidad.

Solución:

Dividiendo ambos términos por 144, la ecuación se nos transforma en su forma ordinaria o canónica reducida:

Como se ha dicho, se ve que el denominador mayor (16) está con la y, es decir, sobre el eje de ordenadas.

En base a la ecuación de este caso, podemos comprobar que:

Ahora hallaremos los focos con la ecuación conocida, basada en el Teorema de Pitágoras:

Y la elipse queda así:

Queda ahora calcular su excentricidad mediante la fórmula:

Mediante la equivalencia de los coeficientes de la ecuación general vista más arriba, se llegaría al mismo resultado de los semiejes. Y también de que se trata de una elipse vertical centrada en el origen de coordenadas.

Ejercicio 4

Dada la ecuación general de una cónica:

Determinar:

a) Si esta ecuación general de una cónica se corresponde con una elipse. Caso de serlo, su posición respecto a los ejes de coordenadas.

b) Transformar la ecuación en forma general en la ecuación ordinaria o canónica.

c) Hallar los semiejes a y b y las coordenadas del centro de la elipse (o₁, o₂).

d) Escribir las ecuaciones paramétricas correspondientes.

Solución:

a) Como A y C tienen signo positivo (9 y 25) esta cónica es una elipse. Como la ecuación general no tiene el término Bxy, no está inclinada o rotada. Al ser A menor que C (9 ≤ 25), es una elipse horizontal. Y como tiene los términos Dx y Ey, el centro no está en ningún eje coordenado.

b) Se hacen transformaciones para obtener en el primer término la suma de los cuadrados de dos binomios:

Se dividen los dos términos por 225 y se obtiene:

Llegando a la forma ordinaria o canónica de una elipse horizontal con el centro fuera de los ejes coordenados, cuya expresión era:

c) A la vista de la ecuación ordinaria, se llega directamente a los semiejes de la elipse (a = 5 y b = 3) y a las coordenadas de su centro (-6, 4):

d) Y las ecuaciones paramétricas son:

A los mismos resultados en los ejes y las coordenadas del centro se hubiera llegado recordando las equivalencias de los coeficientes de la ecuación general, sabiendo que se refieren a una elipse horizontal, porque C ≤ A y no existe el término Bxy:

Ejercicio 5

Sea una elipse de semiejes conocidos, siendo el mayor a=3 cm y el menor b=2 cm. ¿Cuál es su área?

Obteniendo que su área es de 18,85 cm².

Ejercicio 6

Sea una elipse, siendo el semieje mayor a=3 cm y el menor b=2 cm. ¿Cuál es su perímetro? Veamos que se obtiene mediante cada aproximación.

Mediante la primera aproximación, se obtiene que el perímetro es de 16,02 cm.

Aplicando la aproximación de Ramanujan obtenemos que el perímetro es de 15,87 cm.

Ejercicio 7

Hallar la excentricidad de la elipse que tiene como ecuación ordinaria:

La fórmula de la ecuación ordinaria (en configuración horizontal) recordamos que era:

De la que se deduce que:

Sabiendo los dos semiejes ya podemos calcular la excentricidad, usando en este caso la variante que hace uso del teorema de Pitágoras:

Como en la imagen:

Ejercicio 8

Hallar las ecuaciones de las rectas tangente y normal del punto o los puntos con ordenada y_Pi = 2, de la siguiente elipse horizontal, centrada en el origen:

Solución:

Efectivamente, la elipse es horizontal, porque el denominador mayor es el de la x² y no tiene término en xy. Está centrada, al estar solamente las incógnitas en el numerador. Y son dos puntos con esa ordenada, ya que 2 es menor que el semieje menor, b = 3.

Se encuentran las abscisas de estos dos puntos, substituyendo en la ecuación de la elipse la y por 2:

Los puntos buscados son P₁ (-2,98, 2) y P₂ (2,98, 2).

Se aplica la fórmula de la tangente al punto P₁:

Ahora, la ecuación de la normal a P₁:

La ecuación de la tangente al punto P₂ (2,98, 2) será:

Y la de la normal a P₂:

El resultado se refleja en esta imagen: