Media

La media x (también llamada promedio o media aritmética) de un conjunto de datos (X₁,X₂,…,X_N) es una medida de posición central. La definimos como el valor característico de la serie de datos resultado de la suma de todas las observaciones dividido por el número total de datos.

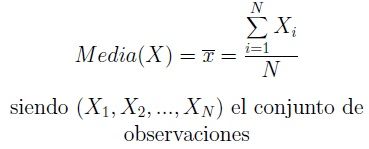
Es decir:

Si se trata de los datos (X₁,X₂,…,X_N) de una muestra, estaremos en la media muestral. Si el conjunto de datos es toda la población, se llama media poblacional. Cuando se trata de la media de una población, este parámetro suele caracterizarse con la letra griega μ. El estadístico media muestral y la medida media poblacional son dos conceptos distintos, ya que el primero es un valor estimado a partir de una muestra mientras que el segundo es un valor medido sobre una población. Pero la fórmula para hallarlos y su valor numérico es el mismo:

Visto desde un punto de vista más conceptual, la media aritmética es el centro de los datos en el sentido numérico, ya que intenta equilibrarlos por exceso y por defecto. Es decir, si sumamos todas las diferencias de los datos a la media es cero.

La media aritmética es muy útil para hacer comparacions entre varias poblaciones.

La desventaja de la media aritmética es que si hay valores extremos alejados, no resulta el promedio más indicado.

Ejercicio 1

Tenemos las edades de los once jugadores de un equipo de fútbol y queremos calcular su media.

Solución:

Para ello, sumamos todas las edades y las dividimos por el número total de elementos, o sea once jugadores.

Media a partir de las frecuencias

En un conjunto de datos discretos agrupados en frecuencias, podemos calcular el promedio o media aritmética a partir de las frecuencias relativas de las observaciones distintas.

El sumatorio está extendido a las observaciones diferentes de los datos.

También con datos discretos agrupados, podemos hallar la media aritmética mediante las frecuencias absolutas.

Ejercicio 2

Tenemos una distribución con valores agrupados en frecuencias. Hallar el valor de la media aritmética mediante las frecuencias absolutas y con las frecuencias relativas. Comprobar que se obtiene el mismo resultado:

Solución:

Se construye la tabla de frecuencias a partir de los datos iniciales de valores y de frecuencias absolutas. Se añade el de las frecuencias relativas y las dos columnas necesarias para la obtención del resultado:

Aplicacando la fórmula de la media de datos agrupados mediante las frecuencias absolutas:

Ahora con la fórmula de la media de datos agrupados, siempre según los resultados de la tabla, mediante las frecuencias relativas:

Se ha obtenido, como se esperaba, el mismo valor, un promedio de 119,24.

Otros tipos de media

La media aritmética es la más conocida. Existen otros tipos de promedios como medida de posición central, que según el tipo de datos será un indicador más representativo o indicado que la media aritmética.

• Media geométrica: se calcula sobre un conjunto de números estrictamente positivos. Es la raíz N-ésima del producto de los N elementos. Está indicada para calcular medias de porcentajes, tantos por uno, puntuaciones o índices. Tiene la ventaja de que no es tan sensible a los valores extremos.
• Media armónica: es el recíproco de la suma de los recíprocos (donde 1/X_i es el recíproco de X_i)) multiplicado por el número de elementos del conjunto. Suele utilizarse principalmente para calcular la media de velocidades, tiempos o en electrónica.
• Media cuadrática: se define como la raíz cuadrada del promedio de los elementos al cuadrado. La media cuadrática es muy útil para variables que toman valores negativos y positivos y su signo no es importante e interesa el valor absoluto del elemento. Por ejemplo, los errores de medida, el valor eficaz de un parámetro sinusoidal en electricidad, etc.
• Media ponderada: consiste en otorgar a cada observación del conjunto de datos unos pesos según la importancia de cada elemento. Tiene numerosas aplicaciones, como el cálculo del IPC (Índice de Precios de Consumo), calcular la nota media de una asignatura ponderando exámenes, trabajos, etc.

Relación entre medias

Existe una relación de orden entre cuatro tipos de media. En esta relación se excluye la media ponderada porque depende de los pesos. Sean:

• H la media armónica
• MG la media geométrica
• x la media aritmética
• RMS la media cuadrática

Entonces:

En esta relación, solamente se cumple la igualdad cuando todos los datos sean iguales, es decir si: x₁ = x₂ = x₃ = … = x_N.

Se da la siguiente relación, en el caso de distribuciones de solamente dos datos, sean estos los que sean:

Cuando en la distribución hay solamente dos datos, la media geométrica es la media geométrica entre la media aritmética y la media armónica.

Esta relación se convierte en una aproximación, cuando, habiendo múltiples valores, estos están muy agrupados en torno a la media.